练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知线段AB,CD分别在两条异面直线上,M,N分别是线段AB,CD的中点,则MN　　　 (AC+BD)(填“>”“<”或“=”).

     

    <

    【解析】如图所示,

    四边形ABCD是空间四边形,而不是平面四边形,要想求MN与AC,BD的关系,必须将它们转化到平面来考虑.取AD的中点为G,再连接MG,NG,在△ABD中,M,G分别是线段AB,AD的中点,则MG∥BD,且MG=BD,同理,在△ADC中,NG∥AC,且NG=AC,又根据三角形的三边关系知,MN<MG+NG,即MN<BD+AC=(AC+BD).

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（九）第二章第六节练习卷（解析版） 题型：解答题

    已知函数f(x)=3ax2+2bx+c,a+b+c=0,且f(0)·f(1)>0.

    (1)求证:-2<<-1.

    (2)若x1,x2是方程f(x)=0的两个实根,求|x1-x2|的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（七）第二章第四节练习卷（解析版） 题型：选择题

    已知函数g(x)=2x-,若f(x)=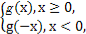则函数f(x)在定义域内(　　)

    (A)有最小值,但无最大值

    (B)有最大值,但无最小值

    (C)既有最大值,又有最小值

    (D)既无最大值,又无最小值

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（一）第一章第一节练习卷（解析版） 题型：选择题

    A={x|x≠1,x∈R}∪{y|y≠2,y∈R},B={z|z≠1且z≠2,z∈R},那么(　　)

    (A)A=B (B)AB

    (C)BA (D)A∩B=?

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷（解析版） 题型：解答题

    直三棱柱ABC-A1B1C1的底面为等腰直角三角形,∠BAC=90°,AB=AC=2,AA1=2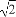,E,F分别是BC,AA1的中点.

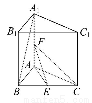
    求(1)异面直线EF和A1B所成的角.

    (2)三棱锥A-EFC的体积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷（解析版） 题型：选择题

    如图是某个正方体的侧面展开图,l1,l2是两条侧面对角线,则在正方体中,l1与l2(　　)

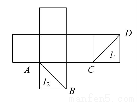
    (A)互相平行

    (B)异面且互相垂直

    (C)异面且夹角为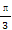

    (D)相交且夹角为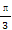

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷（解析版） 题型：解答题

    如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.

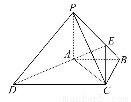
    (1)若PD∥平面EAC,试确定点E在棱PB上的位置.

    (2)在(1)的条件下,求二面角A-CE-P的余弦值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷（解析版） 题型：填空题

    已知l∥α,且l的方向向量为u=(2,m,1),平面α的法向量为v=(1,,2),则m=　　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷（解析版） 题型：填空题

    正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角等于　　　.

     

    查看答案和解析>>

    同步练习册答案