
| A. | $[\frac{π}{12},\frac{5π}{12}]$ | B. | $[\frac{π}{4},\frac{5π}{12}]$ | C. | $[\frac{π}{12},\frac{π}{2})$ | D. | $[\frac{π}{6},\frac{π}{4}]$ |
分析 如图所示,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1-BD-A的平面角.把直线l平移到AM,则∠A1AM=∠MAO=$\frac{π}{4}$.过点A作AP⊥A1O,则AP⊥平面A1BD.利用线面角的定义可得:AM(即直线l)与平面A1BD所成的最大角为∠AMA1.假设$∠{A}_{1}AN=\frac{π}{4}$,AN与直线OP相交于点N,则AN(即直线l)与平面A1BD所成的最小角为∠ANP.
解答 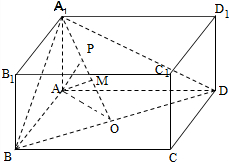 解:如图所示,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1-BD-A的平面角,∴∠AOA1=$\frac{π}{6}$.
解:如图所示,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1-BD-A的平面角,∴∠AOA1=$\frac{π}{6}$.
把直线l平移到AM,则∠A1AM=∠MAO=$\frac{π}{4}$.
过点A作AP⊥A1O,则AP⊥平面A1BD.
∴AM(即直线l)与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=$\frac{5π}{12}$.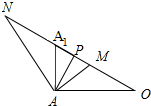
假设$∠{A}_{1}AN=\frac{π}{4}$,AN与直线OP相交于点N,则AN(即直线l)
与平面A1BD所成的最小角为∠ANP=∠PA1A-∠A1AN=$\frac{π}{12}$.
∴直线l与平面A1BD所成角的取值范围是[$\frac{π}{12}$,$\frac{5π}{12}$].
故选:A.
点评 本题考查了二面角的平面角、线面角、三垂线定理、异面直线所成的角,考查了空间想象能力,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 非p或q | B. | p且q | C. | 非p且非q | D. | 非p或非q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com