
【题目】已知![]() ,若在区间
,若在区间![]() 上任取三个数
上任取三个数![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 为边长的三角形,则实数
为边长的三角形,则实数![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】f(x)=x33x+m,求导f′(x)=3x23,由f′(x)=0得到x=1或者x=1,
又x在[0,2]内,∴函数f(x)在区间(0,1)单调递减,在区间(1,2)单调递增,
则f(x)min=f(1)=m2,f(x)max=f(2)=m+2,f(0)=m.
在[0,2]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边的三角形,
三个不同的数a,b,c对应的f(a),f(b),f(c)可以有两个相同。
由三角形两边之和大于第三边,可知最小边长的二倍必须大于最大边长。
由题意知,f(1)=2+m>0…(1),
f(1)+f(1)>f(0),得到4+2m>m…(2),
f(1)+f(1)>f(2),得到4+2m>2+m…(3),
由(1)(2)(3)得到m>6为所求。
实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P
=1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P![]() .
.
(1)求椭圆C的离心率;
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且![]() =
=![]() +
+![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的1 000位上网购物者的年龄情况如图所示.
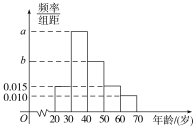
(1)已知[30,40),[40,50),[50,60)三个年龄段的上网购物者人数成等差数列,求a,b的值;
(2)该电子商务平台将年龄在[30,50)内的人群定义为高消费人群,其他年龄段的人群定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1 000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此3人获得代金券总和X(单位:元)的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,短轴的一个端点为
,短轴的一个端点为![]() .过椭圆左顶点
.过椭圆左顶点![]() 的直线
的直线![]() 与椭圆的另一交点为
与椭圆的另一交点为![]() .
.
(1)求椭圆的方程;
(2)若![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin![]() =
=![]() ,则cos
,则cos![]() =
=![]() .其中正确命题的个数为( )
.其中正确命题的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在极坐标系中点C的极坐标为![]() .
.
(1)求出以点C为圆心,半径为2的圆的极坐标方程(写出解题过程)并画出图形;
(2)在直角坐标系中,以圆C所在极坐标系的极点为原点,极轴为x轴的正半轴建立直角坐标系,点P是圆C上任意一点,Q(5,-![]() ),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数①f(x)=4x+![]() -5,②f(x)=|log2 x|-(
-5,②f(x)=|log2 x|-(![]() )x,③f(x)=cos(x+2)-cosx,判断如下两个命题的真假:
)x,③f(x)=cos(x+2)-cosx,判断如下两个命题的真假:
命题甲:f(x)在区间(1,2)上是增函数;
命题乙:f(x)在区间(0,+∞)上恰有两个零点x1,x2,且x1x2<1.
能使命题甲、乙均为真的函数的序号是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com