
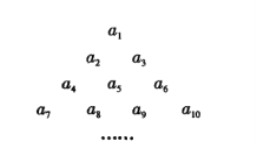
【题目】将各项均为整数的数列![]() 排成如图所示的三角形数阵(第
排成如图所示的三角形数阵(第![]() 行有
行有![]() 个数,同一行中,下标小的数排在左边).
个数,同一行中,下标小的数排在左边).![]() 表示数阵中第
表示数阵中第![]() 行第1列的数.
行第1列的数.
已知数列![]() 为等比数列,且从第3行开始,各行均构成公差为
为等比数列,且从第3行开始,各行均构成公差为![]() 的等差数列,
的等差数列,![]() ,
,![]() ,
,![]() .
.
(1)求数阵中第![]() 行 第
行 第![]() 列的数
列的数 ![]() (用
(用 ![]() 、
、![]() 表示);
表示);
(2)求![]() 的值;
的值;
(3)2013是否在该数阵中,说明理由.
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.4万元/分钟和0.2万元分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是()万元
A.72B.80C.84D.90
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 垂直于向量
垂直于向量![]() ,向量
,向量![]() 垂直于向量
垂直于向量![]() .
.
(1)求向量![]() 与
与![]() 的夹角;
的夹角;
(2)设![]() ,且向量
,且向量![]() 满足
满足![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,随机选取一个向量![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和定点
和定点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一端点为点
直径的一个端点,若另一端点为点![]() ,问
,问![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直平行六面体.命题
为直平行六面体.命题![]() 为正方体;命题
为正方体;命题![]() 的任意体对角线与其不相交的面对角线垂直.则命题
的任意体对角线与其不相交的面对角线垂直.则命题![]() 是命题
是命题![]() 的( )条件 .
的( )条件 .
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图像相邻的两个对称中心之间的距离为
,其图像相邻的两个对称中心之间的距离为![]() ,且有一条对称轴为直线
,且有一条对称轴为直线![]() ,则下列判断正确的是 ( )
,则下列判断正确的是 ( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
D. 函数![]() 的图像关于点
的图像关于点![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com