
【题目】如图,四棱锥P﹣ABCD中,ABCD为矩形,平面PAD⊥平面ABCD. 
(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB= ![]() ,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P﹣ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
【答案】
(1)证明:∵在四棱锥P﹣ABCD中,ABCD为矩形,∴AB⊥AD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥面PAD,∴AB⊥PD
(2)解:过P做PO⊥AD,∴PO⊥平面ABCD,
作OM⊥BC,连接PM
∴PM⊥BC,
∵∠BPC=90°,PB= ![]() ,PC=2,
,PC=2,
∴BC= ![]() ,PM=
,PM= ![]() =
= ![]() =
= ![]() ,BM=
,BM= ![]() =
= ![]() ,
,
设AB=x,∴OM=x∴PO= ![]() ,
,
∴VP﹣ABCD= ![]() ×x×
×x× ![]() ×
× ![]() =
= ![]()
![]() =
= ![]() ,
,
当 ![]() ,即x=
,即x= ![]() ,VP﹣ABCD=
,VP﹣ABCD= ![]() ,
,
建立空间直角坐标系O﹣AMP,如图所示,
则P(0,0, ![]() ),D(﹣
),D(﹣ ![]() ,0,0),C(﹣
,0,0),C(﹣ ![]() ,
, ![]() ,0),M(0,
,0),M(0, ![]() ,0),B(
,0),B( ![]() ,
, ![]() ,0)
,0)
面PBC的法向量为 ![]() =(0,1,1),面DPC的法向量为
=(0,1,1),面DPC的法向量为 ![]() =(1,0,﹣2)
=(1,0,﹣2)
∴cosθ= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() .由图可知二面角为锐角,即cos
.由图可知二面角为锐角,即cos ![]()

【解析】(1)要证AD⊥PD,可以证明AB⊥面PAD,再利用面面垂直以及线面垂直的性质,即可证明AB⊥PD.(2)过P做PO⊥AD得到PO⊥平面ABCD,作OM⊥BC,连接PM,由边长关系得到BC= ![]() ,PM=
,PM= ![]() ,设AB=x,则VP﹣ABCD=
,设AB=x,则VP﹣ABCD= ![]()
![]() ,故当
,故当 ![]() 时,VP﹣ABCD取最大值,建立空间直角坐标系O﹣AMP,利用向量方法即可得到夹角的余弦值.
时,VP﹣ABCD取最大值,建立空间直角坐标系O﹣AMP,利用向量方法即可得到夹角的余弦值.


科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() 过点P且离心率为
过点P且离心率为 ![]() .
. 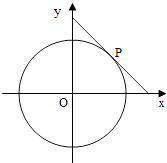
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:



根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有株树木的底部周长小于100cm. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润![]() (元)与年产量
(元)与年产量![]() (吨)满足函数关系
(吨)满足函数关系![]() .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方![]() 元(以下称
元(以下称![]() 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量![]() (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额![]() (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格![]() 是多少?
是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公路AM,AN围成一块顶角为α的角形耕地,其中tanα=-2,在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,![]() km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com