
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=xsinx,x1、x2∈[﹣ ![]() ,
, ![]() ],且f(x1)>f(x2),则下列结论必成立的是( )
],且f(x1)>f(x2),则下列结论必成立的是( )
A.x1>x2
B.x1+x2>0
C.x1<x2
D.x12>x22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的方程为:ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: 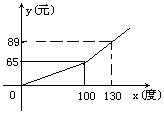
(1)分别写出当0≤x≤100和x≥100时,y与x的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:: ![]() +
+ ![]() =1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
=1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com