
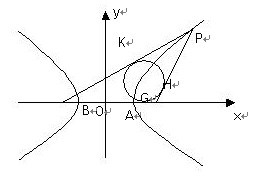
解析:如图,记双曲线在![]() 轴上的两顶点为A(1, 0), B(-1, 0),G为
轴上的两顶点为A(1, 0), B(-1, 0),G为![]() 的内切圆在边
的内切圆在边![]() 上的切点,H为
上的切点,H为![]() 的内切圆在边
的内切圆在边![]() 上的切点,K为
上的切点,K为![]() 的内切圆在边
的内切圆在边![]() 上的切点。则有
上的切点。则有
![]()
![]()
![]() --------------------------------- 5分
--------------------------------- 5分
由双曲线的定义知,G必在双曲线上,于是G与A(1, 0)重合,是定点。
而![]() 。根据圆外一点到该圆的两切点的距离相等,所以
。根据圆外一点到该圆的两切点的距离相等,所以![]() 的内切圆在边
的内切圆在边![]() 上的切点的轨迹是以
上的切点的轨迹是以![]() 为圆心,
为圆心,![]() 为半径的圆弧。------- 10分
为半径的圆弧。------- 10分
因为![]() 是在
是在![]() 第一象限的曲线上移动,当
第一象限的曲线上移动,当![]() 沿双曲线趋于无穷时,与
沿双曲线趋于无穷时,与![]() 轴正向的交角
轴正向的交角![]() 的正切的极限是
的正切的极限是
![]()
即 ![]() 。 故点H的轨迹方程为 (极坐标形式)
。 故点H的轨迹方程为 (极坐标形式)
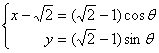 , (
, (![]() ) --------------------------------- 15分
) --------------------------------- 15分
也可以用直角坐标形式。
由于G与A(1, 0)重合,是定点,故该内切圆圆心的轨迹是直线段,方程为
![]() (
(![]() )。 -------------------------------- 20分
)。 -------------------------------- 20分


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2013-2014学年重庆市高三上学期期中考试文科数学试卷(解析版) 题型:填空题
设双曲线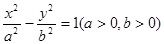 的左、右焦点分别为
的左、右焦点分别为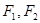 ,离心率为
,离心率为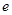 ,过
,过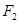 的直线与双曲线的右支交于
的直线与双曲线的右支交于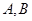 两点,若
两点,若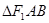 是以
是以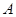 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则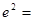 _______.
_______.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
设双曲线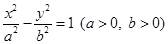 的左、右焦点分别为
的左、右焦点分别为 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,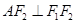 ,原点
,原点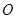 到直线
到直线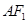 的距离为
的距离为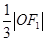 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)
(A)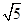 或
或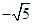 (B)
(B)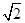 或
或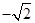 (C)1或
(C)1或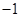 (D)
(D)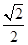 或
或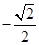
查看答案和解析>>
科目:高中数学 来源:2014届云南省高三上学期第一次月考文科数学试卷(解析版) 题型:选择题
设双曲线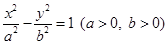 的左、右焦点分别为
的左、右焦点分别为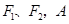 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,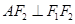 ,原点
,原点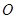 到直线
到直线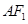 的距离为
的距离为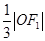 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)
(A)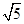 或
或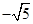 (B)
(B)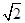 或
或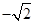 (C)1或
(C)1或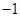 (D)
(D)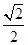 或
或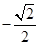
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省高三上学期期末考试数学理卷 题型:选择题
设双曲线 的左、右焦点分别是
的左、右焦点分别是 、
、 ,过点
,过点 的直线交双曲线右支于不同的两点
的直线交双曲线右支于不同的两点 、
、 .若△
.若△ 为正三角形,则该双曲线的离心率为
为正三角形,则该双曲线的离心率为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com