练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．设α，β是两个不同的平面，l，m是两条不同的直线，且l?α，m?β下面命题正确的是（　　）
    A．若l∥β，则α∥βB．若α⊥β，则l⊥mC．若l⊥β，则α⊥βD．若α∥β，则l∥m

    分析 对4个命题分别进行判断，即可得出结论．

    解答 解：对于A，若l∥β，则α∥β或α，β相交，不正确；
    对于B，若α⊥β，则l、m位置关系不定，不正确；
    对于C，根据平面与平面垂直的判定，可知正确；
    对于D，α∥β，则l、m位置关系不定，不正确．
    故选C．

    点评 本题考查了空间线面、面面平行和垂直关系，面面平行的判定定理，线面垂直的定义及其应用，空间想象能力

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知关于x的二次函数f（x）=ax2-2bx+1，设点（a，b）是区域$\left\{\begin{array}{l}x+y-2≤0\\ x+1≥0\\ y+1≥0\end{array}\right.$内的随机点，则函数f（x）在区间[1，+∞）上是增函数的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{8}$C．$\frac{7}{16}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若直线经过两点A（m，2），B（-m，2m-1）且倾斜角为45°，则m的值为（　　）
    A．$\frac{3}{4}$B．1C．2D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知P是椭圆$\frac{x^2}{5}+\frac{y^2}{4}=1$上一点，F1和F2是焦点，若$∠{F_1}P{F_2}={60^0}$，则△PF1F2的面积为（　　）
    A．$5\sqrt{3}$B．$4\sqrt{3}$C．$\frac{{4\sqrt{3}}}{3}$D．$\frac{{5\sqrt{3}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知M是抛物线C：y2=2px（p＞0）上一点，F是抛物线的焦点，∠MFx=60°且|FM|=4．
    （I）求抛物线C的方程；
    （II）已知D（-1，0），过F的直线l交抛物线C与A、B两点，以F为圆心的圆F与直线AD相切，试判断圆F与直线BD的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．集合M={-1，0，1}，N={x∈Z|-1＜x＜1}，则M∩N等于（　　）
    A．{-1，0，1}B．{-1}C．{1}D．{0}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知f（x）=x2-6x+5．
    （Ⅰ）求$f（-\sqrt{2}），f（a）+f（3）$的值；
    （Ⅱ）若x∈[2，6]，求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

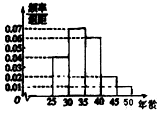    1．2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策，为了了解适龄民众对放开生育二胎政策的态度，某市进行了一次民意调查，参与调查的100位市民中，年龄分布情况如图所示，并得到适龄民众对放开生育二胎政策的态度数据如表：
    生二胎不生二胎合计
    25～35岁451055
    35～50岁301545
    合计7525100
    （1）填写上面的2×2列联表；
    （2）根据调查数据，有多少的把握认为“生二胎与年龄有关”，说明理由；
    （3）调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子，各自家庭都有一个约定：父亲先生二胎，然后儿子生二胎，则这个三个家庭“二胎出生的日期的先后顺序”有多少种？
    参考数据：
     P（K2＞k） 0.15 0.10 0.05 0.010
     k2.072 2.076 3.841 6.635
    （参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知直线m，n和平面α，如果n?α，那么“m⊥n”是“m⊥α”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案