
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,有下列三个命题:
,有下列三个命题:
①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() 、
、
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3.
,则k=﹣3.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为60°.
的夹角为60°.
其中真命题的序号为 . (写出所有真命题的序号)
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有
①刻画一组数据集中趋势的统计量有极差、方差、标准差等;刻画一组数据离散程度统计量有平均数、中位数、众数等.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③有10个阄,其中一个代表奖品,10个人按顺序依次抓阄来决定奖品的归属,则摸奖的顺序对中奖率没有影响.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①x= ![]() 是函数y=2sin(2x﹣
是函数y=2sin(2x﹣ ![]() )的一条对称轴;
)的一条对称轴;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④函数y=cos(x﹣ ![]() )的一个单调增区间是(﹣
)的一个单调增区间是(﹣ ![]() ,
, ![]() )
)
以上四个命题中正确的有(填写正确命题前面的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
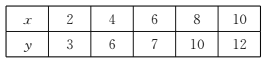
(1)请根据上表数据在网格纸中绘制散点图;
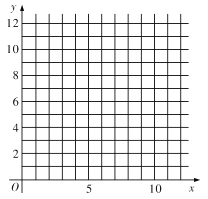
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
(参考公式:  ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x﹣my+3=0和圆C:x2+y2﹣6x+5=0
(1)当直线l与圆C相切时,求实数m的值;
(2)当直线l与圆C相交,且所得弦长为 ![]() 时,求实数m的值.
时,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com