
【题目】设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(MD),有x+l∈D,且f(x+l)![]() f(x),则称f(x)为M上的l高调函数.现给出下列命题:①函数f(x)=2﹣x为R上的1高调函数;②函数f(x)=sin2x为R上的π高调函数;③如果定义域为[﹣1,+∞)的函数f(x)=x2为[﹣1,+∞)上m高调函数,那么实数m的取值范围是[2,+∞);④函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数.其中真命题的个数为( )
f(x),则称f(x)为M上的l高调函数.现给出下列命题:①函数f(x)=2﹣x为R上的1高调函数;②函数f(x)=sin2x为R上的π高调函数;③如果定义域为[﹣1,+∞)的函数f(x)=x2为[﹣1,+∞)上m高调函数,那么实数m的取值范围是[2,+∞);④函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数.其中真命题的个数为( )
A.0B.1C.2D.3
【答案】D
【解析】
①函数f(x)=2﹣x为R上的单调递减函数,可判断其正误;②由正弦函数的性质可知函数f(x)=sin2x为R上的π高调函数;③定义域为[﹣1,+∞)的函数f(x)=x2为[﹣1,+∞)上m高调函数,只有![]() 上至少需要加
上至少需要加![]() ,从而可求实数m的取值范围;④f(x)=lg(|x|+1)
,从而可求实数m的取值范围;④f(x)=lg(|x|+1)![]() ,知函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数,从而可判断④正误;
,知函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数,从而可判断④正误;
①项,由于![]() ,故不满足高调函数定义,故①不正确;
,故不满足高调函数定义,故①不正确;
②项,由![]() ,满足高调函数定义,故②项正确;
,满足高调函数定义,故②项正确;
③项,由函数的定义域知![]() ,即
,即![]() ,
,
又由![]() 得到
得到![]() ,
,
又因为![]() ,故前式恒成立的条件为
,故前式恒成立的条件为![]() ,故③正确;
,故③正确;
④项,因为![]() ,其在区域
,其在区域![]() 上为增函数,
上为增函数,
故![]() ,
,
在区域![]() 上,
上,![]() 为减函数,
为减函数,![]() ,
,
可见![]() 恒成立,故④正确;
恒成立,故④正确;
故选:D


科目:高中数学 来源: 题型:
【题目】已知双曲线C和椭圆![]() 有公共的焦点,且离心率为
有公共的焦点,且离心率为![]() .
.
(1)求双曲线C的方程.
(2)经过点M(2,1)作直线l交双曲线C于A,B两点,且M为AB的中点,求直线l的方程并求弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PD//MA,MA⊥AD,PM⊥平面CDM,MA=AD![]() PD=1.
PD=1.
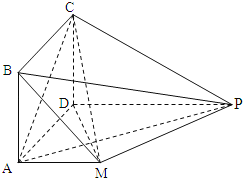
(1)求证:平面ABCD⊥平面AMPD;
(2)求三棱锥A﹣CMP的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】富华中学的一个文学兴趣小组中,三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究,并且他们选择的名家各不相同.三位同学一起来找图书管理员刘老师,让刘老师猜猜他们三人各自的研究对象.刘老师猜了三句话:“①张博源研究的是莎士比亚;②刘雨恒研究的肯定不是曹雪芹;③高家铭自然不会研究莎士比亚.”很可惜,刘老师的这种猜法,只猜对了一句.据此可以推知张博源、高家铭和刘雨恒分别研究的是__________.(A莎士比亚、B雨果、C曹雪芹,按顺序填写字母即可.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=![]() x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
x3-x满足:对于任意的x1,x2∈[0,2],都有|f(x1)-f(x2)|≤a2恒成立,则a的取值范围是( )
A. [-![]() ,
, ![]() ]
]
B. [-![]() ,
, ![]() ]
]
C. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
D. (-∞,- ![]() ]∪[
]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com