
【题目】中新网2016年12月19日电根据预报,今天开始雾霾范围将进一步扩大, ![]() 日夜间至
日夜间至![]() 日,雾霾严重时段部分地区
日,雾霾严重时段部分地区![]() 浓度峰值会超过
浓度峰值会超过![]() 微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等
微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等![]() 个省市在内的地区被雾霾笼罩.
个省市在内的地区被雾霾笼罩. ![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的顆粒物,也称为可人肺颗粒物.
微米的顆粒物,也称为可人肺颗粒物. ![]() 日均值在
日均值在![]() 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在![]() 微克/立方米
微克/立方米![]() 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在![]() 微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的
微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的![]() 监测数据的茎叶图如下:
监测数据的茎叶图如下:

(1)求出这些数据的中位数与极差;
(2)从所给的空气质量不超标的![]() 天的数据中任意抽取
天的数据中任意抽取![]() 天的数据,求这
天的数据,求这![]() 天中恰好有
天中恰好有![]() 天空气质量为一级,另一天空气质量为二级的概率.
天空气质量为一级,另一天空气质量为二级的概率.
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,且a3=﹣6,a6=0.
(1)求{an}的通项公式.
(2)若等比数列{bn}满足b1=8,b2=a1+a2+a3 , 求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ) ![]() 图象上的任意两点,且角φ的终边经过点
图象上的任意两点,且角φ的终边经过点 ![]() ,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当 ![]() 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点. 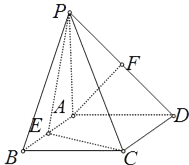
(1)求证:AF∥平面PCE;
(2)求三棱锥C﹣BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
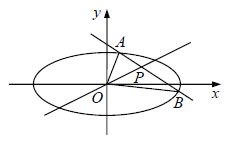
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com