
【题目】已知![]()
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅲ)对一切的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)f(x)单调递减区间是(![]() ,+
,+![]() ),f(x)单调递增区间是(0,
),f(x)单调递增区间是(0, ![]() )
)
(Ⅱ)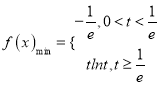 , (Ⅲ)a
, (Ⅲ)a![]() -2
-2
【解析】试题分析:先求出导数的正负确定单调性求出单调区间, 由f(x)单调递减区间是(![]() ,+
,+![]() ),f(x)单调递增区间是(0,
),f(x)单调递增区间是(0, ![]() )求出最值,
)求出最值,![]() ,设
,设![]() ,求出h(x)的最值 ,
,求出h(x)的最值 ,![]()
试题解析:(Ⅰ)![]()
![]()
![]()
![]()
 (Ⅱ)(ⅰ)0<t<t+2<
(Ⅱ)(ⅰ)0<t<t+2<![]() ,t无解;
,t无解;
(ⅱ)0<t<![]() <t+2,即0<t<
<t+2,即0<t<![]() 时,
时,![]() ;
;
(ⅲ)![]()
![]() ,即
,即![]() 时,
时,![]() ,
,![]()
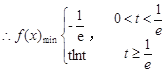
(Ⅲ)由题意:2xlnx≤3x2+2ax-1+2即2xlnx≤3x2+2ax+1
∵x∈(0,+∞),∴a≥lnx-![]() x-
x-![]()
设h(x)= lnx-![]() x-
x-![]() x,在(0,+∞)上恒成立,
x,在(0,+∞)上恒成立,
则![]()
令![]() ,得
,得![]() (舍)
(舍)
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 取得最大值,
取得最大值,![]()
![]() =-2
=-2
![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈线性相关关系,现分别用模型①:
是否有关,现收集了7组观测数据列于下表中,并作出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈线性相关关系,现分别用模型①:![]() 与模型②:
与模型②:![]() 作为产卵数
作为产卵数![]() 和温度
和温度![]() 的回归方程来建立两个变量之间的关系.
的回归方程来建立两个变量之间的关系.
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
|
|
|
|
26 | 692 | 80 | 3.57 |
|
|
|
|
1157.54 | 0.43 | 0.32 | 0.00012 |
其中![]() ,
, ![]()
![]() ,
, ![]() ,
,
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ,
, ![]() .
.

(1)在答题卡中分别画出![]() 关于
关于![]() 的散点图、
的散点图、![]() 关于
关于![]() 的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).
的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).

(2)根据表中数据,分别建立两个模型下建立![]() 关于
关于![]() 的回归方程;并在两个模型下分别估计温度为
的回归方程;并在两个模型下分别估计温度为![]() 时的产卵数.(
时的产卵数.(![]() 与估计值均精确到小数点后两位)(参考数据:
与估计值均精确到小数点后两位)(参考数据: ![]() ,
, ![]() ,
, ![]() )
)
(3)若模型①、②的相关指数计算得分分别为![]() ,
, ![]() ,请根据相关指数判断哪个模型的拟合效果更好.
,请根据相关指数判断哪个模型的拟合效果更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长度为8,
的长度为8, ![]() 的中点到
的中点到![]() 轴的距离为3.
轴的距离为3.
(1)求抛物线的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为6,且抛物线交于
轴上的截距为6,且抛物线交于![]() 两点,连结
两点,连结![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级开设五门大学先修课程,其中属于数学学科的有两门,分别是线性代数和微积分,其余三门分别为大学物理,商务英语以及文学写作,年级要求每名学生只能选修其中一科,该校高二年级600名学生各科选课人数统计如下表:

其中选修数学学科的人数所占频率为0.6,为了了解学生成绩与选课情况之间的关系,用分层抽样的方法从这600名学生中抽取10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(2)从选出的10名学生中随机抽取3人,记![]() 为选择线性代数人数与选择微积分人数差的绝对值,求随机变量
为选择线性代数人数与选择微积分人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com