
【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解到近五个月实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号t | 1 | 2 | 3 | 4 | 5 |
销量(万辆) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
20 | 60 | 60 | 30 | 20 | 10 |
将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式及数据:①回归方程![]() ,其中
,其中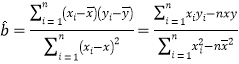 ,
,![]() ,②
,②![]() ,.
,.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线. 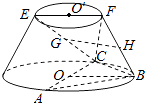
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆C的方程为 ![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(1)当m=3时,判断直线l与C的位置关系;
(2)当C上有且只有一点到直线l的距离等于 ![]() 时,求C上到直线l距离为2
时,求C上到直线l距离为2 ![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,分别是椭圆
,分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若点![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(.(12分)在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为调查高中生选修课的选修倾向与性别关系,随机抽取50名学生,得到如表的数据表:
倾向“平面几何选讲” | 倾向“坐标系与参数方程” | 倾向“不等式选讲” | 合计 | |
男生 | 16 | 4 | 6 | 26 |
女生 | 4 | 8 | 12 | 24 |
合计 | 20 | 12 | 18 | 50 |
(1)根据表中提供的数据,选择可直观判断“选课倾向与性别有关系”的两种,作为选课倾向的变量的取值,并分析哪两种选择倾向与性别有关系的把握大;
附:K2= ![]() .
.
P(k2≤k0) | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(2)在抽取的50名学生中,按照分层抽样的方法,从倾向“平面几何选讲”与倾向“坐标系与参数方程”的学生中抽取8人进行问卷.若从这8人中任选3人,记倾向“平面几何选讲”的人数减去与倾向“坐标系与参数方程”的人数的差为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(cosβ)
D.f(sinα)>f(cosβ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com