
����Ŀ��ij�̳������н���������˿���ÿ��500Ԫ����ѡ��50Ԫ�ֽ��μ�һ�γ齱���齱�������£���1��װ��6������4�����������������һ����������Ϳɻ��100Ԫ�ֽ���������˿ͳ齱�Ľ���������
�������˿�ѡ��μ�һ�γ齱���������100Ԫ�ֽ����ĸ��ʣ�
����ij�˿��ѹ���1500Ԫ����Ϊ�̳���������ϣ���˿�ֱ��ѡ��150Ԫ�ֽ𣬻���ѡ��μ�3�γ齱��˵�����ɣ�
�������˿Ͳμ�10�γ齱�������п��ܻ�ö����ֽ�����
���𰸡��⣺������Ϊ��װ��10���������������һ��Ľ������ ![]() �֣���������Ľ������
�֣���������Ľ������ ![]() �֣�
�֣�
���Թ˿Ͳμ�һ�γ齱���100Ԫ�ֽ����ĸ����� ![]() ��
��
������X��ʾ�˿������γ齱���н��Ĵ�����
���ڹ˿�ÿ�γ齱�Ľ����������ģ���X��B��3��0.4����
����E��X��=np=3��0.4=1.2��
���ڹ˿�ÿ�н�һ�οɻ��100Ԫ�ֽ�������˸ù˿������γ齱�пɻ�õĽ�������
��ֵΪ1.2��100=120Ԫ��
���ڹ˿Ͳμ����γ齱����ֽ����ľ�ֵ120ԪС��ֱ�ӷ��ֵ�150Ԫ��
�����̳�����ϣ���˿Ͳμӳ齱��
������˿Ͳμ�10�γ齱���к���Ĵ���ΪY��
���ڹ˿�ÿ�γ齱�Ľ����������ģ���Y��B��10��0.4����
���ǣ�ǡ��k���н��ĸ���Ϊ ![]() ��k=0��1������10��
��k=0��1������10��
�Ӷ� ![]() ��k=1��2������10��
��k=1��2������10��
��k��4.4ʱ��P��Y=k��1����P��Y=k����
��k��4.4ʱ��P��Y=k��1����P��Y=k����
��P��Y=4�����
���ԣ����п��ܻ�õ��ֽ���Ϊ4��100=400Ԫ��
���ǣ��˿Ͳμ�10�γ齱�����п��ܻ��400Ԫ���ֽ���
��������������Ϊ��װ��10���������������һ��Ľ������ ![]() �֣���������Ľ������
�֣���������Ľ������ ![]() �֣��ɴ�������˿Ͳμ�һ�γ齱���100Ԫ�ֽ����ĸ��ʣ�������X��ʾ�˿������γ齱���н��Ĵ��������ڹ˿�ÿ�γ齱�Ľ����������ģ���X��B��3��0.4�����ɴ�������̳�����ϣ���˿Ͳμӳ齱��������˿Ͳμ�10�γ齱���к���Ĵ���ΪY�����ڹ˿�ÿ�γ齱�Ľ����������ģ���Y��B��10��0.4����ǡ��k���н��ĸ���Ϊ
�֣��ɴ�������˿Ͳμ�һ�γ齱���100Ԫ�ֽ����ĸ��ʣ�������X��ʾ�˿������γ齱���н��Ĵ��������ڹ˿�ÿ�γ齱�Ľ����������ģ���X��B��3��0.4�����ɴ�������̳�����ϣ���˿Ͳμӳ齱��������˿Ͳμ�10�γ齱���к���Ĵ���ΪY�����ڹ˿�ÿ�γ齱�Ľ����������ģ���Y��B��10��0.4����ǡ��k���н��ĸ���Ϊ ![]() ��k=0��1������10���ɴ�������˿Ͳμ�10�γ齱�����п��ܻ��400Ԫ���ֽ�����
��k=0��1������10���ɴ�������˿Ͳμ�10�γ齱�����п��ܻ��400Ԫ���ֽ�����


 �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵΪ���ܼ��ţ���9��Ԫ����һ̨���豸������������һ������Ӫ����2��Ԫ���ӵڶ�����ÿ����Ӫ���þ�����һ������3��Ԫ�����豸ÿ�������������Ϊ21��Ԫ������豸ʹ����n��n��N*�����ӯ���ܶ�ﵽ���ֵ��ӯ������������ȥ�ɱ�������n���ڣ� ��
A.6
B.7
C.8
D.7��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2+bx+c����a��b��c��a+b+c=0������A={m|f��m����0}���� ��
A.����m��A������f��m+3����0
B.����m��A������f��m+3����0
C.����m��A������f��m+3��=0
D.����m��A������f��m+3����0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λ����˶�Ա����ij��ѵ�����Ѹ����10�Σ�ÿ�����еĻ������£�
�� 7 8 7 9 5 4 9 10 7 4
�� 9 5 7 8 7 6 8 6 7 7
����ͨ��������ƣ��ס��Ҷ��˵�����ɼ�˭���ȣ�
�������涨����8�������ϻ���Ϊ���㣬��Ƶ����Ϊ���ʣ��������������ݹ��ƣ�����ڵ�11��
��13������л�û������Ĵ����εķֲ��к�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�Dz���ȵ�������������blna��alnb=a��b���������н��ۣ���a+b��ab��1����a+b��2���� ![]() +
+ ![]() ��2������������ȷ���۵�����ǣ� ��
��2������������ȷ���۵�����ǣ� ��
A.�٢�
B.�٢�
C.�ڢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼij�����������ͼ��ֱ�DZ߳�Ϊ1����������ֱ�������Σ���ü�����������ı����Ϊ�� �� 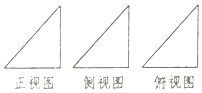
A.![]()
B.![]()
C.![]()
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��ABCD�У�ABCDΪ���Σ�PD����ABCD��PB=2��PB����PCD��45��ǣ�PB����ABD��30��ǣ� 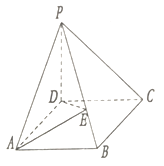
��1����PB���Ƿ����һ��E��ʹPC����ADE��������ȷ��E��λ�ã��������ڣ���˵�����ɣ�
��2����EΪPB�е�ʱ��������P��AE��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���� ![]() ������
������ ![]() ��C1�ϵĵ�P1�ĺ�����Ϊ
��C1�ϵĵ�P1�ĺ�����Ϊ ![]() ����C1�ϵĵ�
����C1�ϵĵ� ![]() ��ֱ��ƽ����x�ᣬ������C2��Qn�㣬�ٴ�C2�ϵĵ�
��ֱ��ƽ����x�ᣬ������C2��Qn�㣬�ٴ�C2�ϵĵ� ![]() ��ֱ��ƽ����y�ᣬ������C1��Pn+1�㣬��Pn��n=1��2��3�����ĺ����깹������{an}��
��ֱ��ƽ����y�ᣬ������C1��Pn+1�㣬��Pn��n=1��2��3�����ĺ����깹������{an}�� 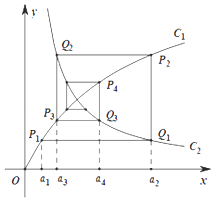
��1��������C1������C2�Ľ������ꣻ
��2������an+1��an֮��Ĺ�ϵ��
��3��֤���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x3+ax�ڣ���1��0��������������
��1����ʵ��a��ȡֵ��ΧA��
��2����aΪA����Сֵʱ����������{an}���㣺a1�ʣ���1��0������2an+1=f��an��������ѧ���ɷ�֤��an�ʣ���1��0�������ж�an+1��an�Ĵ�С��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com