
设f(x)=lg(x2+ax+a-1),
①f(x)有最小值;
②当a=0时,f(x)的值域为R;
③当a>0时,f(x)在区间[2,+∞)上有反函数;
④若f(x)在[2,+∞)上单调递增,则a≥-4;其中正确的是________.
科目:高中数学 来源:2004年高考北京四中全真模拟试卷——数学 题型:044
已知定义在R上的函数f(x)=lg(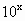 +1)+3x
+1)+3x
(1)设g(x)是R上的奇函数,h(x)是R上的偶函数,且满足f(x)=g(x)+h(x),试求g(x)与h(x);
(2)设a、b∈R,证明a+b>0是f(a)+f(b)>f(-a)+f(-b)的充分必要条件.
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高三数学 苏教版(新课标·2004年初审) 苏教版 题型:044
设f(x)=lg![]() ,如果当x∈(-∞,1)时f(x)有意义,求实数a的取值范围.
,如果当x∈(-∞,1)时f(x)有意义,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届山东省日照市高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
设f(x)=lg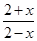 ,则f
,则f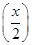 +f
+f 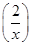 的定义域为( )
的定义域为( )
A.(-4,0)∪(0,4) B.(-4,-1)∪(1,4)
C.(-2,-1)∪(1,2) D.(-4,-2)∪(2,4)
查看答案和解析>>
科目:高中数学 来源:云南省玉溪一中09-10学年高一上学期期中考试 题型:解答题
设F(x)=f(x)-g(x),其中f(x)=lg(x-1),并且仅当(x0,y0)在y=lg(x-1)的图象上时,(2x0,2y0)在y=g(x)的图象上。
(1) 写出g(x)的函数解析式
(2) 当x在什么区间时,F(x)≥0?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com