
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
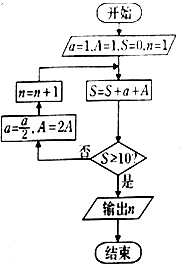
分析 模拟程序的运行,依次写出每次循环得到的a,A,n,S的值,可得当S=$\frac{135}{8}$时满足条件S≥10,退出循环,输出n的值为4.
解答 解:模拟程序的运行,可得:
a=1,A=1,S=0,n=1,
S=2;
不满足条件S≥10,执行循环体,a=$\frac{1}{2}$,A=2,n=2,S=$\frac{9}{2}$,
不满足条件S≥10,执行循环体,a=$\frac{1}{4}$,A=4,n=3,S=$\frac{35}{4}$,
不满足条件S≥10,执行循环体,a=$\frac{1}{8}$,A=8,n=4,S=$\frac{135}{8}$,
满足条件S≥10,退出循环,输出n的值为4.
故选:B.
点评 本题考查的知识点是循环结构,当循环次数不多时,多采用模拟循环的方法,本题属于基础题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
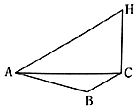 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{-\frac{1}{2}}}$ | B. | y=x-2 | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com