
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)当![]() 时,求证:存在实数
时,求证:存在实数![]() 使
使![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)先根据题意可得![]() 处的切线
处的切线![]() 的斜率为2,从而求得a(2)对于存在问题可根据题意赋值验证,当
的斜率为2,从而求得a(2)对于存在问题可根据题意赋值验证,当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;当
;当![]() 时分析函数单调性,得函数最小值,若最小值小于1即得证
时分析函数单调性,得函数最小值,若最小值小于1即得证
试题解析:
(Ⅰ)![]() ,
,
因为曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,
所以切线![]() 的斜率为2,
的斜率为2,
所以![]() ,
,
所以![]() .
.
(Ⅱ)法1:当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;
;
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
所以在![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递减;
上递减;
![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递增
上递增
所以![]()
![]() 是
是![]() 的极小值.
的极小值.
由函数![]() 可得
可得![]() ,
,
由![]() 可得
可得![]() ,
,
所以![]() ,
,
综上,若![]() ,存在实数
,存在实数![]() 使
使![]() .
.
(Ⅱ)法2:当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;
;
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
所以在![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递减;
上递减;
![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递增.
上递增.
所以![]()
![]() 是
是![]() 的极小值.
的极小值.
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]()
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以当![]() 时
时![]() ,
,
所以![]() ,
,
综上,若![]() ,存在实数
,存在实数![]() 使
使![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F. 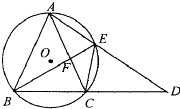
(1)判断BE是否平分∠ABC,并说明理由;
(2)若AE=6,BE=8,求EF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过椭圆
经过椭圆![]()
![]() 的焦点.
的焦点.
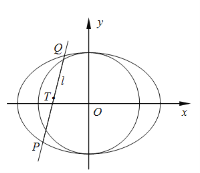
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为弦
为弦![]() 的中点,
的中点,![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点. 
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额![]() (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
(Ⅰ)如果采取方案一,求![]() 的概率;
的概率;
(Ⅱ)分别计算方案二、方案三的平均数![]() 和方差
和方差![]() ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的![]() 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
方案二 | 方案三 | 合计 | |
男性 | 12 | ||
女性 | 40 | ||
合计 | 82 | 100 |
附:![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的偶函数f(x),满足对任意x∈R都有f(t)=f(2﹣t)且x∈(0,1]时,f(x)= ![]() ,a=f(
,a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(
),c=f( ![]() ),用“<“表示a,b,c的大小关系是 .
),用“<“表示a,b,c的大小关系是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
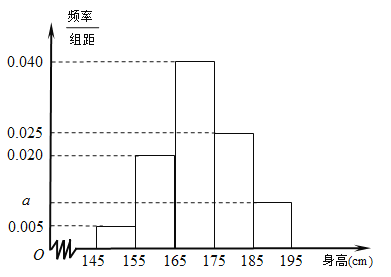
【题目】某中学随机选取了![]() 名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
(Ⅰ)求![]() 的值及样本中男生身高在
的值及样本中男生身高在![]() (单位:
(单位: ![]() )的人数;
)的人数;
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高;
(Ⅲ)在样本中,从身高在![]() 和
和![]() (单位:
(单位: ![]() )内的男生中任选两人,求这两人的身高都不低于
)内的男生中任选两人,求这两人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”. 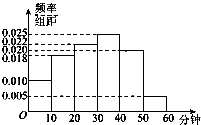
(1)样本中“手机迷”有多少人?
(2)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“手机迷”与性别有关?
(3)将上述调查所得到的频率视为概率.现在从该地区大量大学 生中,采用随机抽样方法每次抽取1名大学生,抽取3次,经调查一名“手机迷”比“非手机迷”每月的话费平均多40元,记被抽取的3名大学生中的“手机迷”人数为X,且设3人每月的总话费比“非手机迷”共多出Y元,若每次抽取的结果是相互独立的,求X的分布列和Y的期望EY
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com