
从某小组的2名女生和3名男生中任选2人去参加一项公益活动.
(1)求所选2人中恰有一名男生的概率;
(1)求所选2人中至少有一名女生的概率.
(1) ;(2)
;(2)
解析试题分析:先将2名女生和3名男生分别用字母表示,将随机抽取2人所包含的基本事件一一例举,(1)再将抽取的2人中恰有一男一女所包含的事件一一例举,根据古典概型概率公式可求其概率。(1)将抽取的2人中至少有一名女生所包含的事件一一例举,根据古典概型概率公式可求其概率。
试题解析:解析设2名女生为a1,a2,3名男生为b1,b2,b3,从中选出2人的基本事件有:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3),共10种.
(1)设“所选2人中恰有一名男生”的事件为A,则A包含的事件有:(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共6种,
∴ ,
,
故所选2人中恰有一名男生的概率为 .
.
(2)设“所选2人中至少有一名女生”的事件为B,则B包含的事件有:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共7种,
∴ ,
,
故所选2人中至少有一名女生的概率为 .
.
考点:古典概型概率。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
黄山旅游公司为了体现尊师重教,在每年暑假期间对来黄山旅游的全国各地教师和学生,凭教师证和学生证实行购买门票优惠.某旅游公司组织有22名游客的旅游团到黄山旅游,其中有14名教师和8名学生.但是只有10名教师带了教师证,6名学生带了学生证.
(1)在该旅游团中随机采访3名游客,求恰有1人持有教师证且持有学生证者最多1人的概率;
(2)在该团中随机采访3名学生,设其中持有学生证的人数为随机变量ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在一次游戏中,①摸出3个白球的概率,②获奖的概率;
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
寒假期间,我市某校学生会组织部分同学,用“10分制”随机调查“阳光花园”社区人们的幸福度,现从调查人群中随机抽取16名,如果所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶);若幸福度分数不低于8.5分,则该人的幸福度为“幸福”.
(1)求从这16人中随机选取3人,至少有2人为“幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线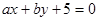 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
(1)图中纵坐标 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com