
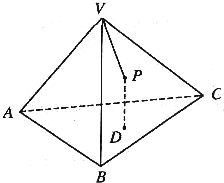
 如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )
如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是( )2
| ||
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
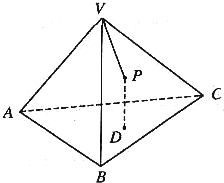 如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是
如图,P是正四面体V-ABC的面VBC上一点,点P到平面ABC距离与到点V的距离相等,则动点P的轨迹是 的椭圆
的椭圆查看答案和解析>>
科目:高中数学 来源:上海高考真题 题型:解答题

 PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)查看答案和解析>>
科目:高中数学 来源:2007-2008学年重庆市南开中学高三(下)3月月考数学试卷(理科)(解析版) 题型:选择题
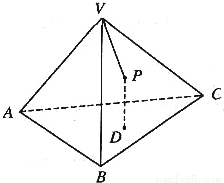
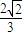 的椭圆
的椭圆查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com