
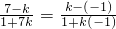 …(4分)
…(4分) …(6分)
…(6分)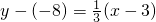 …(7分)
…(7分)

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
(本小题满分12分)标准椭圆![]() 的两焦点为
的两焦点为![]() ,
,![]() 在椭圆上,且
在椭圆上,且![]() . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线![]() 的方向向量为
的方向向量为![]() ,若
,若![]() 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与![]() 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
查看答案和解析>>
科目:高中数学 来源:2002-2003学年北京市北大附中高二(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com