
 (a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l:
(a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l: 截得的弦长等于2,则a= .
截得的弦长等于2,则a= .  截得的弦长等于2,求出a与圆心到直线l:
截得的弦长等于2,求出a与圆心到直线l: 的距离d之间的等量关系即可求出a.
的距离d之间的等量关系即可求出a. ,0),因为双曲线的渐近线y=
,0),因为双曲线的渐近线y= x⇒
x⇒ x-ay=0.
x-ay=0. =
= ,
, 截得的弦长等于2,
截得的弦长等于2, 的距离d=1=
的距离d=1= ⇒a2=2又a>0,故a=
⇒a2=2又a>0,故a= .
. .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三10月月考理科数学卷 题型:选择题
设圆C的圆心在双曲线 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线 截得的弦长等于2,则
截得的弦长等于2,则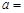 ( )
( )
(A)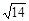 (B)
(B) (C)
(C) (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:北京市宣武区2010年高三第一次质量检测数学(文)试题 题型:选择题
设圆C的圆心在双曲线 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线 截得的弦长等于2,则a的值为 ( )
截得的弦长等于2,则a的值为 ( )
A. B.
B. C.2 D.3
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com