
【题目】已知函数![]() .
.
(1)判断![]() 的奇偶性,并证明;
的奇偶性,并证明;
(2)用定义证明函数![]() 在
在![]() 上单调递减;
上单调递减;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】现对一块边长8米的正方形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (米),
(米),![]() 的面积记为
的面积记为![]() (平方米),其余部分面积记为
(平方米),其余部分面积记为![]() (平方米).
(平方米).
(1)当![]() (米)时,求
(米)时,求![]() 的值;
的值;
(2)求函数![]() 的最大值;
的最大值;
(3)该场地中![]() 部分改造费用为
部分改造费用为![]() (万元),其余部分改造费用为
(万元),其余部分改造费用为![]() (万元),记总的改造费用为W(万元),求W取最小值时x的值.
(万元),记总的改造费用为W(万元),求W取最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的电子新产品未上市时,原定每件售价100元,经过市场调研发现,该电子新产品市场潜力很大,该公司决定从第一周开始销售时,该电子产品每件售价比原定售价每周涨价4元,5周后开始保持120元的价格平稳销售,10周后由于市场竞争日益激烈,每周降价2元,直到15周结束,该产品不再销售.
(Ⅰ)求售价![]() (单位:元)与周次
(单位:元)与周次![]() (
(![]() )之间的函数关系式;
)之间的函数关系式;
(Ⅱ)若此电子产品的单件成本![]() (单位:元)与周次
(单位:元)与周次![]() 之间的关系式为
之间的关系式为![]() ,
,![]() ,
,![]() ,试问:此电子产品第几周的单件销售利润(销售利润
,试问:此电子产品第几周的单件销售利润(销售利润![]() 售价
售价![]() 成本)最大?
成本)最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() ,且
,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)设函数 ,记
,记![]() (
(![]() ,
,![]() ).探究是否存在正整数
).探究是否存在正整数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有满足条件的正整数
恒成立?若存在,求出所有满足条件的正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考结论:设![]() 均为常数,函数
均为常数,函数![]() 的图象关于点
的图象关于点![]() 对称的充要条件是
对称的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AOB是一块半径为r的扇形空地,![]() .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若![]() ,设
,设![]()
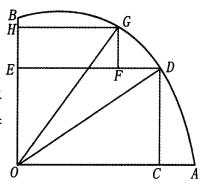
(Ⅰ)记活动场地与停车场占地总面积为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅱ)当![]() 为何值时,可使活动场地与停车场占地总面积最大.
为何值时,可使活动场地与停车场占地总面积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com