
分析 (1)由题意知A(a,0),从而可得P($\frac{a}{2}$,$\frac{a}{2}$),从而得方程组$\left\{\begin{array}{l}{\frac{(\frac{a}{2})^{2}}{{a}^{2}}+\frac{(\frac{a}{2})^{2}}{{b}^{2}}=1}\\{\frac{1}{2}•a•\frac{a}{2}=3}\end{array}\right.$,从而解得;
(2)由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+3{y}^{2}-12=0}\end{array}\right.$化简可得(3k2+1)x2+6kmx+3m2-12=0,从而可得△=(6km)2-4(3k2+1)(3m2-12)>0,化简可得m2-4(3k2+1)<0,再由韦达定理可得x1+x2=-$\frac{6km}{3{k}^{2}+1}$,y1+y2=$\frac{2m}{3{k}^{2}+1}$,从而可得$\frac{2-\frac{m}{3{k}^{2}+1}}{\frac{3km}{3{k}^{2}+1}}$•k=-1,从而化简可得m=-(3k2+1),从而解得.
解答 解:(1)由题意知,A(a,0),
故线段OA的中垂线为x=$\frac{a}{2}$,
故线段OA的中垂线与直线y=x的交点P($\frac{a}{2}$,$\frac{a}{2}$),
故$\left\{\begin{array}{l}{\frac{(\frac{a}{2})^{2}}{{a}^{2}}+\frac{(\frac{a}{2})^{2}}{{b}^{2}}=1}\\{\frac{1}{2}•a•\frac{a}{2}=3}\end{array}\right.$,
解得,a2=12,b2=4,
故椭圆C的方程为$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1;
(2)∵$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+3{y}^{2}-12=0}\end{array}\right.$,
∴(3k2+1)x2+6kmx+3m2-12=0,
∴△=(6km)2-4(3k2+1)(3m2-12)>0,
即m2-4(3k2+1)<0,
设M(x1,y1),N(x2,y2);
故x1+x2=-$\frac{6km}{3{k}^{2}+1}$,
y1+y2=k(x1+x2)+2m=$\frac{2m}{3{k}^{2}+1}$,
故MN的中点的坐标为(-$\frac{3km}{3{k}^{2}+1}$,$\frac{m}{3{k}^{2}+1}$),
而B(0,2),
故$\frac{2-\frac{m}{3{k}^{2}+1}}{\frac{3km}{3{k}^{2}+1}}$•k=-1,
故m=-(3k2+1),
故m2-4(3k2+1)<0可化为m2+4m<0,
解得,-4<m<0.
点评 本题考查了学生的化简运算能力及椭圆与直线的位置关系的判断与应用.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {α|α=475°+k•360°,k∈Z} | B. | α|α=97°+k•360°,k∈Z} | ||
| C. | α|α=263°+k•360°,k∈Z} | D. | α|α=-263°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
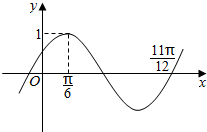 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )| A. | [2kπ-$\frac{π}{6}$,2kπ$+\frac{π}{3}$] | B. | [2k$π+\frac{π}{3}$,2kπ$+\frac{5π}{6}$] | C. | [kπ$+\frac{π}{3}$,kπ$+\frac{5π}{6}$] | D. | [kπ$-\frac{π}{6}$,kπ$+\frac{π}{3}$], |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com