练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】学校将从4名男生和4名女生中选出4人分别担任辩论赛中的一、二、三、四辩手，其中男生甲不适合担任一辩手，女生乙不适合担任四辩手．现要求：如果男生甲入选，则女生乙必须入选．那么不同的组队形式有_________种．

    【答案】

    【解析】分析：分三种情况讨论，分别求出甲乙都入选、甲不入选，乙入选、甲乙都不入选,，相应的情况不同的组队形式的种数，然后求和即可得出结论.

    详解：若甲乙都入选，则从其余人中选出人，有种，男生甲不适合担任一辩手，女生乙不适合担任四辩手，则有种，故共有 种；

    若甲不入选，乙入选，则从其余人中选出人，有种，女生乙不适合担任四辩手，则有种，故共有种；

    若甲乙都不入选，则从其余6人中选出人，有种，再全排，有种，故共有种，综上所述，共有，故答案为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】将函数f（x）=sin2x的图象沿x轴向右平移φ（φ＞0）个单位长度后得到函数g（x）的图象，若函数g（x）的图象关于y轴对称，则当φ取最小的值时，g（0）= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，和是函数的图象与轴的个相邻交点的横坐标，且当时，取得最大值.

    （1）求数的表达式；

    （2）将函数的图象上的每一点的横坐标变为原来的倍（纵坐标不变），得到函数的图象，再将函数的图象向右平移个单位，得到函数的图象.

    ①求函数的解析式；

    ②求函数在区间上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小明的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：

    0～2000

    2001～5000

    5001～8000

    8001～10000

    男

    1

    2

    3

    6

    8

    女

    0

    2

    10

    6

    2

    （1）若采用样本估计总体的方式，试估计小明的所有微信好友中每日走路步数超过5000步的概率；

    （2）已知某人一天的走路步数超过8000步时被系统评定为“积极型”，否则为“懈怠型”.根据小明的统计完成下面的列联表，并据此判断是否有以上的把握认为“评定类型”与“性别”有关？

    积极型

    懈怠型

    总计

    男

    女

    总计

    附：

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抽样统计甲、乙两名学生的5次训练成绩（单位：分），结果如下：

    学生

    第1次

    第2次

    第3次

    第4次

    第5次

    甲

    65

    80

    70

    85

    75

    乙

    80

    70

    75

    80

    70

    则成绩较为稳定（方差较小）的那位学生成绩的方差为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP=OC，PA⊥PD．求证：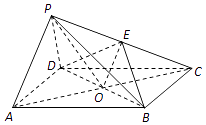
    （1）直线PA∥平面BDE；
    （2）平面BDE⊥平面PCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某公司为郑州园博园生产某特许商品，该公司年固定成本为10万元，每生产千件需另投入2 .7万元，设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元，

    且，

    (I)写出年利润W(万元〉关于该特许商品x(千件）的函数解析式；

    〔II〕年产量为多少千件时，该公司在该特许商品的生产中所获年利润最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，已知2bcosC=acosC+ccosA．

    （1）求角C的大小；

    （2）若b=2，c=，求a及△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面向量 ， ， 满足| |= ，| |=1， =﹣1，且 ﹣ 与 ﹣ 的夹角为 ，则| |的最大值为（ ）
    A.
    B.2
    C.
    D.4

    查看答案和解析>>

    同步练习册答案