
【题目】已知点P(2,-1).
(1)求过P点且与原点距离为2的直线l的方程;
(2)求过P点且与原点距离最大的直线l的方程,最大距离是多少?
【答案】
(1)解:①当l的斜率k不存在时显然满足要求,
∴l的方程为x=2;
②当l的斜率k存在时,设l的方程为y+1=k(x-2),
即kx-y-2k-1=0.
由点到直线距离公式得 ![]() ,
,
∴k= ![]() ,∴l的方程为3x-4y-10=0.
,∴l的方程为3x-4y-10=0.
故所求l的方程为x=2或3x-4y-10=0.
(2)解:易知过P点与原点O距离最大的直线是过P点且与 PO垂直的直线,由l⊥OP得klkOP=-1,所以 ![]() =-
=- ![]() =2.
=2.
由直线方程的点斜式得y+1=2(x-2),
即2x-y-5=0.
即直线2x-y-5=0是过P点且与原点O距离最大的直线,
最大距离为 ![]() .
.
【解析】(1)先对直线l的斜率的存在性进行讨论,当直线的斜率存在时利用斜截式设出直线l的方程,再由嗲到直线的距离公式列出方程,解方程即可求得斜率k的值,从而求得所需直线的方程;(2)先分析出满足距离最大直线的条件是:过P点且与PO垂直的直线,从而利用两直线垂直求得直线l的斜率,从而利用点斜式求得直线l的方程,也易求得最大距离.


科目:高中数学 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 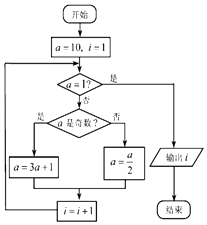
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】到直线3x-4y+1=0的距离为3,且与此直线平行的直线方程是 ( )
A.3x-4y+4=0
B.3x-4y+4=0或3x-4y-2=0
C.3x-4y+16=0
D.3x-4y+16=0或3x-4y-14=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:方程 ![]() =1表示焦点在x轴上的椭圆,q:双曲线
=1表示焦点在x轴上的椭圆,q:双曲线 ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ).
).
(1)若椭圆 ![]() =1的焦点和双曲线
=1的焦点和双曲线 ![]() =1的顶点重合,求实数m的值;
=1的顶点重合,求实数m的值;
(2)若“p∧q”是真命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com