
【题目】下列命题中,错误命题是
A. “若![]() ,则
,则![]() ”的逆命题为真
”的逆命题为真
B. 线性回归直线![]() 必过样本点的中心
必过样本点的中心![]()
C. 在平面直角坐标系中到点![]() 和
和![]() 的距离的和为
的距离的和为![]() 的点的轨迹为椭圆
的点的轨迹为椭圆
D. 在锐角![]() 中,有
中,有![]()
科目:高中数学 来源: 题型:
【题目】如图所示多面体![]() ,其底面
,其底面![]() 为矩形且
为矩形且![]() ,四边形
,四边形![]() 为平行四边形,点
为平行四边形,点![]() 在底面
在底面![]() 内的投影恰好是
内的投影恰好是![]() 的中点.
的中点.
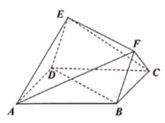
(1)已知![]() 为线段
为线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 大小为
大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为正方形,![]() ,E,F分别是棱PC,AB的中点.
,E,F分别是棱PC,AB的中点.
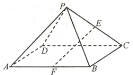
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直线EF与平面PAB所成角的正弦值.
,求直线EF与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为20米,圆心角![]() 的扇形展示台,展示台分成了四个区域:三角形
的扇形展示台,展示台分成了四个区域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米
).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米![]() ,紫龙卧雪30元/米
,紫龙卧雪30元/米![]() ,朱砂红霜40元/米
,朱砂红霜40元/米![]() .
.
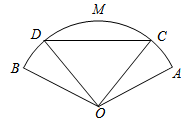
(1)设![]() ,试建立日效益总量
,试建立日效益总量![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试探求![]() 为何值时,日效益总量达到最大值.
为何值时,日效益总量达到最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区年龄在25~55岁的人员中,随机抽出100人,了解他们对今年两会的热点问题的看法,绘制出频率分布直方图如图所示,则下列说法正确的是( )

A. 抽出的100人中,年龄在40~45岁的人数大约为20
B. 抽出的100人中,年龄在35~45岁的人数大约为30
C. 抽出的100人中,年龄在40~50岁的人数大约为40
D. 抽出的100人中,年龄在35~50岁的人数大约为50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于方程为![]() 的曲线
的曲线![]() 给出以下三个命题:
给出以下三个命题:
(1)曲线![]() 关于原点对称;(2)曲线
关于原点对称;(2)曲线![]() 关于
关于![]() 轴对称,也关于
轴对称,也关于![]() 轴对称,且
轴对称,且![]() 轴和
轴和![]() 轴是曲线
轴是曲线![]() 仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点
仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点![]() ,都在曲线
,都在曲线![]() 上,则四边形
上,则四边形![]() 每一条边的边长都大于2;
每一条边的边长都大于2;
其中正确的命题是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若![]() ,
,![]() ,且
,且![]() ,则称
,则称![]() 调和分割
调和分割![]() .已知平面上的点
.已知平面上的点![]() 调和分割点
调和分割点![]() ,则下列说法正确的是
,则下列说法正确的是
A. ![]() 可能线段
可能线段![]() 的中点
的中点
B. ![]() 可能线段
可能线段![]() 的中点
的中点
C. ![]() 可能同时在线段
可能同时在线段![]() 上
上
D. ![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com