练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙两人参加普法知识竞赛，共有10道不同的题目，其中选择题6道，判断题4道，甲、乙两人各抽一道（不重复）.
    （1）甲抽到选择题，乙抽到判断题的概率是多少？
    （2）甲、乙二人中至少有一人抽到选择题的概率是多少？

    （1）甲抽到选择题，乙抽到判断题的概率是.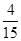
    （2）甲、乙二人中至少有一人抽到选择题的概率是.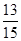

    解析试题分析：
    思路分析：（1）按古典概型概率的计算方法，确定基本事件空间事件数，确定事件“甲抽到选择题，乙抽到判断题”含有的基本事件数，然后计算比值。
    （2）利用“甲、乙二人中至少有一人抽到选择题”的对立事件“甲、乙二人都抽到判断题”计算概率，能起到“化繁为简”的作用。
    解：（1）甲、乙两人从10道题中不重复各抽一道，共有种抽法      3分
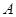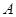    记“甲抽到选择题，乙抽到判断题”为事件，则事件含有的基本事件数为
                             5分
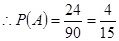                        7分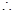
    甲抽到选择题，乙抽到判断题的概率是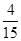.           8分
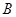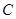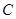    （2）记“甲、乙二人中至少有一人抽到选择题”为事件，其对立事件为“甲、乙二人都抽到判断题”，记为事件，则事件含有的基本事件数为  10分

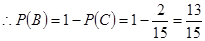                       12分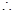
    甲、乙二人中至少有一人抽到选择题的概率是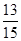.        13分
    考点：古典概型概率的计算，对立事件概率计算公式。
    点评：中档题，对事件的认识与理解，是准确解题的基础，准确计算事件数是解题的关键。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球，现从中有放回地随机抽取2个小球，抽取的球的编号分别记为、，记.
    （Ⅰ）求取最大值的概率；
    （Ⅱ）求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某经销商试销A、B两种商品一个月（30天）的记录如下：

    日销售量（件）
         		0
         		1
         		2
         		3
         		4
         		5
     
    商品A的频数
         		2
         		5
         		7
         		7
         		5
         		4
     
    商品B的频数
         		4
         		4
         		6
         		8
         		5
         		3
     
    若售出每种商品1件均获利40元，将频率视为概率。
    （Ⅰ）求B商品日销售量不超过3件的概率；
    （Ⅱ）由于某种原因，该商家决定只选择经销A、B商品的一种，你认为应选择哪种商品，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市准备从7名报名者（其中男5人，女3人）中选3人参加三个副局长职务竞选.
    （1）设所选3人中女副局长人数为，求的分布列及数学期望.
    （2）若选派三个副局长依次到、、三个局商上任，求局是男局长的情况下，局是女副局长的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某小组共有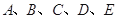五位同学，他们的身高（单位:米）以及体重指标（单位:千克/米2）如下表所示：

     
    		A
    		B
    		C
    		D
    		E
    身高
    		1．69
    		1．73
    		1．75
    		1．79
    		1．82
    体重指标
    		19．2
    		25．1
    		18．5
    		23．3
    		20．9
    （1）从该小组身高低于1．80的同学中任选2人，求选到的2人身高都在1．78以下的概率；
    （2）从该小组同学中任选2人，求选到的2人的身高都在1．70以上且体重指标都在[18．5，23．9)中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    一个不透明的袋子中装有4个形状相同的小球，分别标有不同的数字2，3，4，，现从袋中随机摸出2个球，并计算摸出的这2个球上的数字之和，记录后将小球放回袋中搅匀，进行重复试验。记A事件为“数字之和为7”.试验数据如下表

    摸球总次数
    		10
    		20
    		30
    		60
    		90
    		120
    		180
    		240
    		330
    		450
    “和为7”出现的频数
    		1
    		9
    		14
    		24
    		26
    		37
    		58
    		82
    		109
    		150
    “和为7”出现的频率
    		0.10
    		0.45
    		0.47
    		0.40
    		0.29
    		0.31
    		0.32
    		0.34
    		0.33
    		0.33
    （参考数据：）
    （Ⅰ）如果试验继续下去，根据上表数据，出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率，并求的值；
    （Ⅱ）在（Ⅰ）的条件下，设定一种游戏规则：每次摸2球，若数字和为7，则可获得奖金7元，否则需交5元。某人摸球3次，设其获利金额为随机变量元，求的数学期望和方差。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
    性别与看营养说明列联表 单位: 名

     
         		男
         		女
         		总计
     
    看营养说明
         		50
         		30
         		80
     
    不看营养说明
         		10
         		20
         		30
     
    总计
         		60
         		50
         		110
     
    （1）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为10的样本，问样本中看与不看营养说明的女生各有多少名?
    （2）根据以上列联表，能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系？
    下面的临界值表供参考：

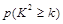         		0.15
         		0.10
         		0.05
         		0.025
         		0.010
         		0.005
         		0.001
     

         		2.072
         		2.706
         		3.841
         		5.024
         		6.635
         		7.879
         		10.828
     
     (参考公式：，其中)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “肇实，正名芡实，因肇庆所产之芡实颗粒大、药力强，故名。”某科研所为进一步改良肇实，为此对肇实的两个品种（分别称为品种A和品种B）进行试验．选取两大片水塘，每大片水塘分成n小片水塘，在总共2n小片水塘中，随机选n小片水塘种植品种A，另外n小片水塘种植B．
    （1）假设n=4，在第一大片水塘中，种植品种A的小片水塘的数目记为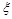，求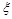的分布列和数学期望；
    （2）试验时每大片水塘分成8小片，即n=8，试验结束后得到品种A和品种B在每个小片水塘上的每亩产量（单位：kg/亩）如下表：

     号码
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    		8
    品种A
    		101
    		97
    		92
    		103
    		91
    		100
    		110
    		106
    品种B
    		115
    		107
    		112
    		108
    		111
    		120
    		110
    		113
    分别求品种A和品种B的每亩产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物)：
    61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
    (1)完成频率分布表；
    (2)作出频率分布直方图；
    (3)根据国家标准，污染指数在0～50之间时，空气质量为优；在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染．
    请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价．

    查看答案和解析>>

    同步练习册答案