
分析 由题意可得,函数在区间[m,n]上为增函数,则$\left\{\begin{array}{l}{f(m)=-{m}^{2}+2m=3m}\\{f(n)=-{n}^{2}+2n=3n}\end{array}\right.$,解得即可.
解答 解:函数f(x)=-x2+2x的对称轴方程式x=1,
由题意可得,函数在区间[m,n]上为增函数,则$\left\{\begin{array}{l}{f(m)=-{m}^{2}+2m=3m}\\{f(n)=-{n}^{2}+2n=3n}\end{array}\right.$,
则m,n时方程-x2+2x=3x的两个根,
∴m+n=-1,
故答案为:-1
点评 本题主要考查二次函数的性质应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | m=-1或m=2 | B. | m=2 | C. | m=-1 | D. | m=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10) | B. | (5,6) | C. | (10,11) | D. | (20,22) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
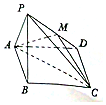 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
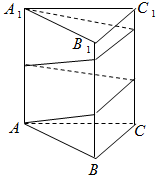 已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )| A. | 16cm | B. | 12$\sqrt{3}$cm | C. | 24$\sqrt{3}$cm | D. | 26cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
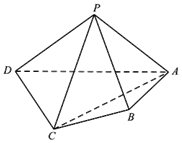 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com