已知二次函数y=g(x)的图象经过点O(0,0)、A(m,0)与点P(m+1,m+1),设函数f(x)=(x-n)g(x)在x=a和x=b处取到极值,其中m>n>0,b<a.
(1)求g(x)的二次项系数k的值;
(2)比较a,b,m,n的大小(要求按从小到大排列);
(3)若m+n≤2,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
解:(1)由题意可设g(x)=kx(x-m),k≠0,
又函数图象经过点P(m+1,m+1),则m+1=k(m+1)(m+1-m),得k=1.…(2分)
(2)由(1)可得y=g(x)=x(x-m)=x
2-mx.
所以f(x)=(x-n)g(x)=x(x-m)(x-n)=x
3-(m+n)x
2+mnx,
f′(x)=3x
2-2(m+n)x+mn,…(4分)
函数f(x)在x=a和x=b处取到极值,
故f′(a)=0,f′(b)=0,…(5分)
∵m>n>0,
∴f′(m)=3m
2-2(m+n)m+mn=m
2-mn=m(m-n)>0…(7分)
f′(n)=3n
2-2(m+n)n+mn=n
2-mn=n(n-m)<0
又b<a,故b<n<a<m. …(8分)
(3)设切点Q(x
0,y
0),则切线的斜率
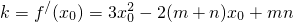
又

,所以切线的方程是

…(9分)
又切线过原点,故

所以

,解得x
0=0,或
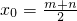
. …(10分)
两条切线的斜率为

,

,
由
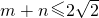
,得(m+n)
2≤8,
∴
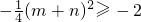
,
∴
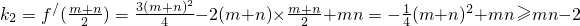
,
…(12分)
所以
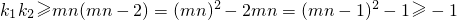
,
又两条切线垂直,故k
1k
2=-1,所以上式等号成立,有
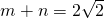
,且mn=1.
所以

. …(14分)
分析:(1)由题意可设g(x)=kx(x-m),k≠0,根据题中条件:函数图象经过点P(m+1,m+1),列出等式得k值;
(2)由(1)可得y=g(x)=x(x-m)=x
2-mx.从而f(x)=x
3-(m+n)x
2+mnx,再利用导数研究此函数的极值,结合取值极值的条件得出a,b,m,n的大小.
(3)设切点Q(x
0,y
0),利用导数的几何意义得到切线的斜率及切线的方程,再结合基本不等式及两条切线垂直,求出
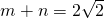
,mn=1,从而得到y=f(x)的解析式.
点评:本小题主要考查二次函数的性质、函数导数的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

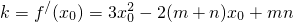
 ,所以切线的方程是
,所以切线的方程是 …(9分)
…(9分)
 ,解得x0=0,或
,解得x0=0,或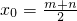 . …(10分)
. …(10分) ,
, ,
,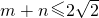 ,得(m+n)2≤8,
,得(m+n)2≤8,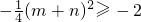 ,
,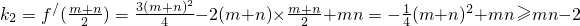 ,
,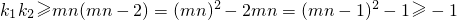 ,
,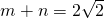 ,且mn=1.
,且mn=1. . …(14分)
. …(14分)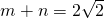 ,mn=1,从而得到y=f(x)的解析式.
,mn=1,从而得到y=f(x)的解析式.

 期末集结号系列答案
期末集结号系列答案