
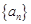 满足
满足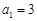 ,
,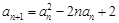 .
.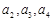 ;
;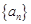 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想. ;证明祥见解析.
;证明祥见解析.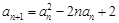 令n=1,再将
令n=1,再将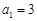 代入即可求得
代入即可求得 的值;再令n=2并将
的值;再令n=2并将 的值就可求得
的值就可求得 的值;最后再令n=2并将
的值;最后再令n=2并将 的值就可求得
的值就可求得 的值;(2)由已知及(1)的结果,可猜想出
的值;(2)由已知及(1)的结果,可猜想出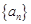 的一个通项公式;用数学归纳法证明时应注意格式:①验证
的一个通项公式;用数学归纳法证明时应注意格式:①验证 时猜想正确;②作归纳假设:假设当
时猜想正确;②作归纳假设:假设当 时,猜想成立,在此基础上来证明
时,猜想成立,在此基础上来证明 时猜想也成立,注意在此证明过程中要充分利用已知条件找出
时猜想也成立,注意在此证明过程中要充分利用已知条件找出 之间的关系,并一定要用到假设当
之间的关系,并一定要用到假设当 时的结论;最后一定要下结论.
时的结论;最后一定要下结论.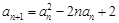 ,依次得
,依次得 ,
,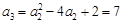 ,
, , 6分
, 6分 . 7分
. 7分 时,
时, ,猜想成立; 8分
,猜想成立; 8分 时,猜想成立,即有
时,猜想成立,即有 , 9分
, 9分 时,有
时,有 ,
, 时猜想也成立, 13分
时猜想也成立, 13分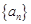 通项公式为
通项公式为 . 14分
. 14分

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:解答题
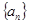 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.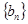 是等差数列;
是等差数列;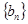 前n项和Sn及
前n项和Sn及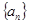 通项an.
通项an.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
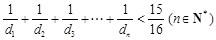 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com