Question

已知使函数f（x）=x³-ax²-1（0≤a≤M）存在整数零点的实数a恰有3个，则M的取值范围是    ．

Answer 1

【答案】分析：由f（x）=0，解得．再利用a≥0即可得出x的取值范围，从最小的整数x讨论开始即可得出M的取值范围．
解答：解：当x=0时，f（0）=-1≠0，即x=0不是函数f（x）的零点；
当x≠0时，由f（x）=0，解得．
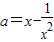
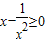
∵a≥0，∴，解得x≥1．
当x=1时，a=0，满足题意；
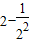
当x=2时，a==，满足题意；
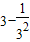
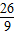
当x=3时，a==，满足题意；
当x=4时，a==．
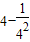
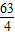
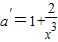
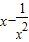
又∵＞0，∴当x≥1时，等单调递增．
又∵函数f（x）存在整数零点的实数a恰有3个，∴M的取值范围是．
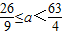
故答案为．
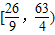
点评：利用函数零点的意义把问题正确等价转化，熟练掌握分类讨论的思想方法是解题的关键．