
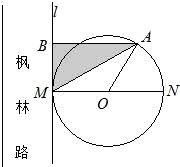
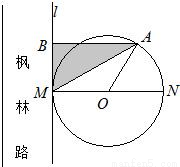
 长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)
长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米) MB•AB=
MB•AB= ×100sinθ×(100-100cosθ)
×100sinθ×(100-100cosθ) ,cosθ=-1(舍去),此时θ=
,cosθ=-1(舍去),此时θ=
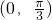 时,S′>0;
时,S′>0; 时,S取得极大值,即S最大值=3750
时,S取得极大值,即S最大值=3750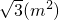
 m2
m2

科目:高中数学 来源: 题型:
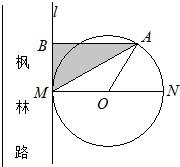 长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)
长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省四市九校高三第一次联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com