
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】有10所学校,每所都选派若干名男生和若干名女生举行跳棋比赛,同一学校的选手不比赛,不同学校的选手不论男女在两人之间都要进行一场比赛. 在两个男生或两个女生之间的比赛总局数与男生和女生之间的比赛总局数与男生和女生之间的比赛总局数至多相差1,而男生的总人数和女生的总人数也至多相差1. 求证:至少有7所学校选派的男生和女生人数相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点与短轴的一个端点恰好围成一个面积为
的两个焦点与短轴的一个端点恰好围成一个面积为![]() 的等边三角形.
的等边三角形.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() 、
、![]() ,右焦点为
,右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的动点,直线
的动点,直线![]() 与椭圆
与椭圆![]() 在点
在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得数据如下表(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(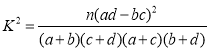 ,其中
,其中 ![]() )
)
抗倒伏数据如下:
143 147 147 151 153 153 157 159 160 164 166 169 174 175 175
180 188 188 192 195 195 199 203 206 206
易倒伏数据如下:
151 167 175 178 181 182 186 186 187 190 190 193 194 195 198
199 199 202 202 203
(1)完成 2×2 列联表,并说明能否在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,再从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,求X的分布列(概率用组合数算式表示);
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n为给定的正整数,t为给定的实数,设(t+x)n=a0+a1x+a2x2+…+anxn.
(1)当n=8时.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求数列{an}中的最大值;
,求数列{an}中的最大值;
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() :“
:“![]() ,使得
,使得![]() ”,则非
”,则非![]() :“
:“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方形花圃被分成5份.
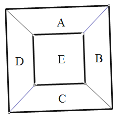
(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若将6个不同的盆栽都摆放入这5个部分,且要求每个部分至少有一个盆栽,问有多少种不同的放法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com