
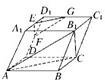
 如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.
如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点. 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
 对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则(
对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则(| AB |
| AD |
| AE |
| A、4 | ||
| B、8 | ||
C、2
| ||
D、4
|
查看答案和解析>>
科目:高中数学 来源: 题型:
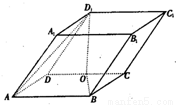
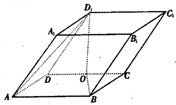 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:044
如图,平行六面体
ABCD-A1B1C1D1的底面为正方形,点A1在底面的射影O在AB上,已知侧棱A1A与底面ABCD成45°角,A1A=a.求二面角A1-AC-B的平面角的正切值.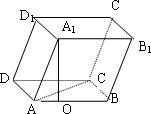
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
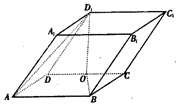 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.查看答案和解析>>
科目:高中数学 来源:2011年四川省乐山市高三第三次调查研究数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com