练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．sin40°（tan190°-$\sqrt{3}$）=-1．

    分析 化切为弦，然后利用两角差的正弦及诱导公式化简求值．

    解答 解：sin40°（tan190°-$\sqrt{3}$）=sin40°（tan10°$-\sqrt{3}$）
    =sin40°（$\frac{sin10°}{cos10°}-\sqrt{3}$）=sin40°•$\frac{sin10°-\sqrt{3}cos10°}{cos10°}$
    =sin40°$•\frac{-2sin50°}{cos10°}$=-$\frac{2sin40°cos40°}{cos10°}$=$-\frac{sin80°}{cos10°}=-1$．
    故答案为：-1．

    点评 本题考查三角函数的化简求值，考查诱导公式及两角差的正弦，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知等差数列{an}的前n项和为Sn，a2=2，S5=15，则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和为（　　）
    A．$\frac{2016}{2017}$B．$\frac{2017}{2016}$C．$\frac{2017}{2018}$D．$\frac{2018}{2017}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．关于函数f（x）=x2-2x+1的零点，下列说法正确的是（　　）
    A．因为f（0）?f（2）＞0，所以f（x）在（0，2）内没有零点
    B．因为1是f（x）的一个零点，所以f（0）?f（2）＜0
    C．由于f（x）在区间（-∞，0）上单调递减，所以f（x）在（-∞，0）内有唯一的一个零点
    D．以上说法都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知角θ的终边过点P（-12，5），则cosθ=（　　）
    A．$\frac{5}{13}$B．$-\frac{12}{13}$C．$\frac{12}{13}$D．$-\frac{5}{13}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

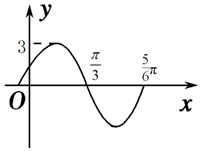    17．函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则（　　）
    A．f（x）的一个对称中心为$（\frac{4π}{3}，0）$B．f（x）的图象关于直线$x=-\frac{1}{12}π$ 对称
    C．f（x）在$[-π，-\frac{π}{2}]$上是增函数D．f（x）的周期为$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x-m，1≤x＜3}\\{3（x-m）（x-2m），x≥3}\end{array}\right.$，
    （1）若m=2，求f（x）的最小值；
    （2）若f（x）恰有2个零点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．正三棱锥V-ABC中，VB=$\sqrt{7}$，BC=2$\sqrt{3}$，则二面角V-AB-C的大小为60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

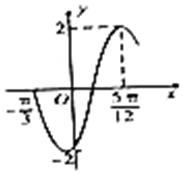    11．已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示．
    （Ⅰ）求f（x）的解析式；
    （Ⅱ）求f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设a，b是非零实数，若a＞b，则一定有（　　）
    A．$a+\frac{1}{b}＞b+\frac{1}{a}$B．$\frac{1}{{a{b^2}}}＞\frac{1}{{{a^2}b}}$C．$\frac{1}{a}＜\frac{1}{b}$D．ab＞b2

    查看答案和解析>>

    同步练习册答案