
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
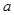 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为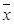 ,定义事件
,定义事件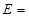 {
{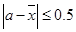 ,且函数
,且函数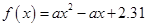 没有零点},求事件
没有零点},求事件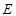 发生的概率.
发生的概率.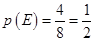 .
.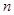 辆,由题意得
辆,由题意得 ,从而得到
,从而得到 . 计算得到
. 计算得到 =400;
=400;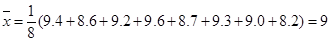
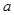 对应的基本事件的总数为
对应的基本事件的总数为 个,
个,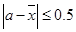 ,且函数
,且函数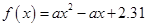 没有零点建立不等式组求得
没有零点建立不等式组求得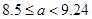 ,进一步得到
,进一步得到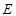 发生当且仅当
发生当且仅当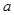 的值为:8.6,9.2,8.7,9.0共4个,
的值为:8.6,9.2,8.7,9.0共4个,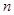 辆,由题意得:
辆,由题意得: ,所以
,所以 .
. 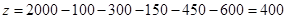 4分
4分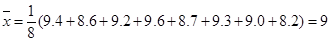 6分
6分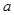 对应的基本事件的总数为
对应的基本事件的总数为 个,
个,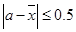 ,且函数
,且函数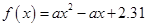 没有零点
没有零点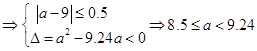 10分
10分
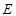 发生当且仅当
发生当且仅当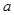 的值为:
的值为: 共4个,
共4个, 12分
12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
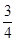 ,
,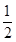 ,
,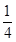 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.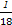 | B.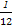 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.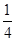 | B. | C.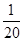 | D.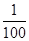 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com