
【题目】已知过点P(4,0)的动直线与抛物线C:![]() 交于点A,B,且
交于点A,B,且![]() (点O为坐标原点).
(点O为坐标原点).
(1)求抛物线C的方程;
(2)当直线AB变动时,x轴上是否存在点Q使得点P到直线AQ,BQ的距离相等,若存在,求出点Q坐标,若不存在,说明理由.
【答案】(1)![]() =
=![]() ;(2)
;(2)![]() 轴上存在点
轴上存在点![]() ,使得点
,使得点![]() 到直线
到直线![]() ,
,![]() 的距离相等.
的距离相等.
【解析】
(1)设过点![]() 的动直线为
的动直线为![]() =
=![]() ,联立抛物线的方程,设
,联立抛物线的方程,设![]() ,
,![]() ,运用韦达定理,结合向量的数量积的坐标表示,化简可得
,运用韦达定理,结合向量的数量积的坐标表示,化简可得![]() ,进而得到抛物线方程;
,进而得到抛物线方程;
(2)![]() 轴上假设存在点
轴上假设存在点![]() 符合题意,由题意可得
符合题意,由题意可得![]() =
=![]() ,运用直线的斜率公式和韦达定理,化简可得
,运用直线的斜率公式和韦达定理,化简可得![]() 的值,即可判断存在性.
的值,即可判断存在性.
(1)设过点![]() 的动直线为
的动直线为![]() =
=![]() ,
,
代入抛物线![]() =
=![]() ,可得
,可得![]() =
=![]() ,
,
设![]() ,
,![]() ,
,
可得![]() =
=![]() ,
,
由![]() 可得
可得![]() =
=![]() =
=![]() ,
,
解得![]() =
=![]() ,则抛物线的方程为
,则抛物线的方程为![]() =
=![]() ;
;
(2)当直线![]() 变动时,
变动时,![]() 轴上假设存在点
轴上假设存在点![]() 使得点
使得点![]() 到直线
到直线![]() ,
,![]() 的距离相等,
的距离相等,
由角平分线的判定定理可得![]() 为
为![]() 的角平分线,即有
的角平分线,即有![]() =
=![]() ,
,
由(1)可得![]() =
=![]() ,
,![]() =
=![]() ,
,
则![]() ,
,
化为![]() =
=![]() ,
,
即为![]() =
=![]() ,
,
化简可得![]() =
=![]() ,
,
则![]() 轴上存在点
轴上存在点![]() ,使得点
,使得点![]() 到直线
到直线![]() ,
,![]() 的距离相等.
的距离相等.


科目:高中数学 来源: 题型:
【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: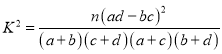 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
甲套设备的样本的频率分布直方图
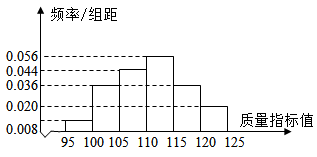
乙套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 6 | 19 | 18 | 5 | 1 |
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: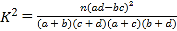 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00-23:00这一时间段内顾客0这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的频率分布直方图如下图所示,其中时间段7:00 11:00,11:00 15:00,15:00 ~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
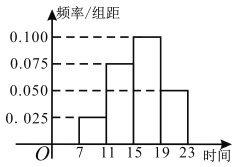
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)现从10月1日在该商场购买商品的顾客中随机抽取100名顾客,经统计有男顾客 40人,其中10人购物时刻在[19,23](夜晚),女顾客60人,其中50人购物时刻在[7,19)(白天),根据提供的统计数据,完成下面的2×2列联表,并判断是否有90%的把握认为“男顾客更喜欢在夜晚购物”?
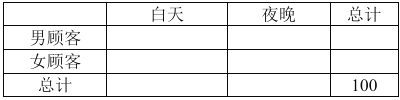
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() (e为自然对数的底数)时,
(e为自然对数的底数)时,
(i)若![]() 在
在![]() 上恰有两个不同的零点,求实数m的取值范围;
上恰有两个不同的零点,求实数m的取值范围;
(ii)若![]() (
(![]() ),求
),求![]() 在
在![]() 上的最大值;
上的最大值;
(2)当![]() 时,
时,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .求证:
.求证: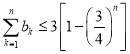 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com