
【题目】已知函数 ![]() .
.
(1)若对任意的 ![]() ,均有
,均有 ![]() ,求
,求 ![]() 的取值范围;
的取值范围;
(2)若对任意的 ![]() ,均有
,均有 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解: ![]() ,
,
由 ![]() ,得
,得 ![]() .
. ![]() ,当
,当 ![]() 时,
时, ![]() ,要使
,要使 ![]() 恒成立,只需
恒成立,只需 ![]() ,解得
,解得 ![]() .
.
当 ![]() 时,
时, ![]() ,要使
,要使 ![]() 恒成立,只需
恒成立,只需 ![]() ,矛盾.
,矛盾.
综上 ![]() 的取值范围是
的取值范围是 ![]() .
.
(2)解: ![]()
![]() ,
,
要使 ![]() 恒成立,只需
恒成立,只需 ![]() ,
,
则 ![]() ,因为
,因为 ![]() ,
, ![]() ,
,
所以只需 ![]() 恒成立,则所求的m的取值范围为
恒成立,则所求的m的取值范围为 ![]() .
.
【解析】(1)利用二倍角公式和两角和差的正弦公式整理已知的代数式得到f(x) 的解析式,结合已知条件给出的取值范围根据正弦型函数的最值情况可得出 f ( x 1) ∈ [ 0 , 2 ],同理可得出当 m ≥ 0 时, g ( x2 ) ∈ [ 2 m + 2 , ![]() m + 2 ] ,由已知要满足题意中的恒成立则有0 ≥
m + 2 ] ,由已知要满足题意中的恒成立则有0 ≥ ![]() m + 2,解出m的取值范围即可。(2)同理结合二倍角的余弦公式整理原函数的代数式得到f(x) 的最简形式,根据题意f ( x ) ≥ g ( x ) 恒成立得到关于cos(x+
m + 2,解出m的取值范围即可。(2)同理结合二倍角的余弦公式整理原函数的代数式得到f(x) 的最简形式,根据题意f ( x ) ≥ g ( x ) 恒成立得到关于cos(x+![]() )的不等式借助角的取值范围结合余弦函数的最值求出cos(x+
)的不等式借助角的取值范围结合余弦函数的最值求出cos(x+![]() )的取值范围,进而得到要满足 m > 2 [cos(x+
)的取值范围,进而得到要满足 m > 2 [cos(x+![]() ) + 1 ] 恒成立所以m ≥ 3 .
) + 1 ] 恒成立所以m ≥ 3 .
【考点精析】解答此题的关键在于理解二倍角的正弦公式的相关知识,掌握二倍角的正弦公式:![]() ,以及对二倍角的余弦公式的理解,了解二倍角的余弦公式:
,以及对二倍角的余弦公式的理解,了解二倍角的余弦公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1 , F2 , 线段OF1 , OF2的中点分别为B1 , B2 , 且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2 , 求直线l的方程 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量对岸A,B两点的距离,沿河岸选取C,D两点,测得CD=2km,∠CDB=∠ADB=30°,∠ACD=60°,∠ACB=45°,求A,B两点的距离. 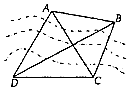
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,a2=2,b1=2,且对任意的正整数i,j,k,l,当i+j=k+l时,都有ai+bj=ak+bl , 则 ![]() 的值是( )
的值是( )
A.2012
B.2013
C.2014
D.2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则 ![]() 的值为( )
的值为( )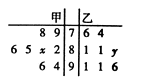
A.9
B.10
C.11
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线 ![]() ,两个平面
,两个平面 ![]() ,给出下面四个命题:
,给出下面四个命题:
① ![]() ,
, ![]() ;②
;② ![]() ,
, ![]() ,
, ![]() ;
;
③ ![]() ,
, ![]() ;④
;④ ![]() ,
, ![]() ,
, ![]()
其中正确命题的序号是( )
A.①④
B.②④
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时, ![]() ,函数
,函数 ![]() ,则关于x的不等式f(x)<g(x)的解集为( )
,则关于x的不等式f(x)<g(x)的解集为( )
A.(﹣2,﹣1)∪(﹣1,0)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2},B={x|(x2+ax)(x2+ax+2)=0},记集合A中元素的个数为n(A),定义m(A,B)= ![]() ,若m(A,B)=1,则正实数a的值是 .
,若m(A,B)=1,则正实数a的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com