
【题目】下列说法正确的有_________.
①函数![]() 的一个对称中心为
的一个对称中心为![]() ;
;
②在![]() 中,
中, ![]() 是
是![]() 的中点,则
的中点,则![]() ;
;
③在![]() 中,
中, ![]() 是
是![]() 的充要条件;
的充要条件;
④定义![]() ,已知
,已知![]() ,则
,则![]() 的最大值为
的最大值为![]() .
.
【答案】①②③④
【解析】 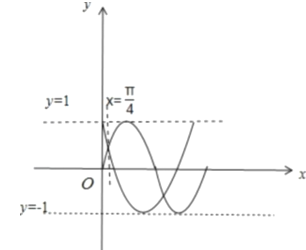
①对于函数![]() ,令
,令![]() ,求得
,求得![]() ,故函数
,故函数![]() 的图象的一个对称中心为
的图象的一个对称中心为![]() ,故①正确;②在
,故①正确;②在![]() 中,
中, ![]() 是
是![]() 的中点,则
的中点,则![]() ,故②正确;③在
,故②正确;③在![]() 中,
中, ![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,故③正确;④定义
,故③正确;④定义![]() ,已知
,已知![]() ,画出
,画出![]() 和
和![]() 的图象,如图所示,则由图可知,当
的图象,如图所示,则由图可知,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,故④正确,故答案为①②③④.
,故④正确,故答案为①②③④.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查向量的线性运算及三角函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】2017年3月14日,“![]() 共享单车”终于来到芜湖,
共享单车”终于来到芜湖,![]() 共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于
共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的
,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的![]() 名市民,并根据这
名市民,并根据这![]() 名市民对该项目满意程度的评分(满分
名市民对该项目满意程度的评分(满分![]() 分),绘制了如下频率分布直方图:
分),绘制了如下频率分布直方图:

(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于![]() 分的市民中随机抽取
分的市民中随机抽取![]() 人进行座谈,求这
人进行座谈,求这![]() 人评分恰好都在
人评分恰好都在![]() 的概率;
的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=
,PB= ![]()
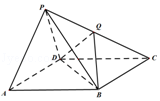
(Ⅰ)求证:平面PAD⊥平面ABCD;
(Ⅱ)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中PM2.5浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化.2017年除夕18时和初一2时,国家环保部门对8个城市空气中PM2.5浓度监测的数据如表(单位:微克/立方米).
除夕18时PM2.5浓度 | 初一2时PM2.5浓度 | |
北京 | 75 | 647 |
天津 | 66 | 400 |
石家庄 | 89 | 375 |
廊坊 | 102 | 399 |
太原 | 46 | 115 |
上海 | 16 | 17 |
南京 | 35 | 44 |
杭州 | 131 | 39 |
(Ⅰ)求这8个城市除夕18时空气中PM2.5浓度的平均值;
(Ⅱ)环保部门发现:除夕18时到初一2时空气中PM2.5浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
(Ⅲ)记2017年除夕18时和初一2时以上8个城市空气中PM2.5浓度的方差分别为s12和s22 , 比较s12和s22的大小关系(只需写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=pe﹣x+x+1(p∈R). (Ⅰ)当实数p=e时,求曲线y=f(x)在点x=1处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)当p=1时,若直线y=mx+1与曲线y=f(x)没有公共点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,
垂直,![]() 为
为![]() 的中点,如图2.
的中点,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,若椭圆
,若椭圆![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且圆
两点,且圆![]() 在椭圆
在椭圆![]() 内的弧长为
内的弧长为![]() .
.
(1)求![]() 的值;
的值;
(2)过椭圆![]() 的中心作两条直线
的中心作两条直线![]() 交椭圆
交椭圆![]() 于
于![]() 和
和![]() 四点,设直线
四点,设直线![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,且
,且![]() .
.
①求直线![]() 的斜率;
的斜率;
②求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com