

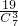 =
= .
. .
.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
从红桃2、3、4、5和梅花2、3、4、5这8张扑克牌中取出4张排成一排,如果取出的4张扑克牌所标的数字之和等于14,则不同的排法共有 种(用数字作答).
查看答案和解析>>
科目:高中数学 来源:2010年广东省高三上学期期中考试文科数学卷 题型:解答题
(本小题满分12分)
从1、2、3、4、5、8、9这7个数中任取三个数,共有35种不同的取法(两种取法不同,指的是一种取法中至少有一个数与另一种取法中的三个数都不相同)。
(Ⅰ)求取出的三个数能够组成等比数列的概率;
(Ⅱ)求取出的三个数的乘积能被2整除的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com