
【题目】已知函数![]()
![]() .
.
(1)![]() 时,求
时,求![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)![]() 且
且![]() ,
, ![]() 均恒成立,求实数
均恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间是![]() ,单调减区间是
,单调减区间是![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据![]() ,对
,对![]() 求导,再令
求导,再令![]() ,再根据定义域,求得
,再根据定义域,求得![]() 在
在![]() 上是单调递减函数,由
上是单调递减函数,由![]() ,即可求出
,即可求出![]() 在
在![]() 上的单调区间;(2)通过
上的单调区间;(2)通过![]() 时,化简不等式,
时,化简不等式, ![]() 时,化简不等式,设
时,化简不等式,设![]() ,利用函数的导数,通过导函数的符号,判断单调性,推出
,利用函数的导数,通过导函数的符号,判断单调性,推出![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() 符合题意;
符合题意; ![]() 时,
时, ![]() 时,都出现矛盾结果;得到
时,都出现矛盾结果;得到![]() 的集合.
的集合.
试题解析:(1)![]() 时,
时, ![]() ,设
,设![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上是单调递减函数,即
上是单调递减函数,即![]() 在
在
![]() 上是单调递减函数,
上是单调递减函数,
∵![]() ∴
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
∴在![]() 上
上![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ;
;
(2)![]() 时,
时, ![]() ,即
,即![]() ;
;
![]() 时,
时, ![]() ,即
,即![]() ;
;
设![]() ,
,
则![]()
![]() 时,
时, ![]()
∵![]()
∴![]() 在
在![]() 上单调递增
上单调递增
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
∴![]() 符合题意;
符合题意;
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时, ![]() ,与
,与![]() 时,
时, ![]() 矛盾;舍
矛盾;舍
![]() 时,设
时,设![]() 为
为![]() 和0中的最大值,当
和0中的最大值,当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减
上单调递减
∴当![]() 时,
时, ![]() ,与
,与![]() 时,
时, ![]() 矛盾;舍
矛盾;舍
综上, ![]()


科目:高中数学 来源: 题型:
【题目】甲、乙两名同学准备参加考试,在正式考试之前进行了十次模拟测试,测试成绩如下:
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)画出甲、乙两人成绩的茎叶图,求出甲同学成绩的平均数和方差,并根据茎叶图,写出甲、乙两位同学平均成绩以及两位同学成绩的中位数的大小关系的结论;
(2)规定成绩超过127为“良好”,现在老师分别从甲、乙两人成绩中各随机选出一个,求选出成绩“良好”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 是双曲线
是双曲线![]() 上的两个动点,动点
上的两个动点,动点![]() 满足
满足![]() ,直线
,直线![]() 与直线
与直线![]() 斜率之积为2,已知平面内存在两定点
斜率之积为2,已知平面内存在两定点![]() 、
、![]() ,使得
,使得![]() 为定值,则该定值为________
为定值,则该定值为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )在点
)在点![]() 处的切线斜率为1.
处的切线斜率为1.
(1)用![]() 表示
表示![]() ;
;
(2)设![]() ,若
,若![]() 对定义域内的
对定义域内的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的前提下,如果![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃![]() ,梅花
,梅花![]() ,方片
,方片![]() 以及黑桃
以及黑桃![]() ,让明、小红、小张、小李四个人进行猜测:
,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
小红说:第2个盒子里面饭的是梅花![]() ,第3个盒子里放的是黑桃
,第3个盒子里放的是黑桃![]() ;
;
小张说:第4个盒子里面放的是黑桃![]() ,第2个盒子里面放的是方片
,第2个盒子里面放的是方片![]() ;
;
小李说:第4个盒子里面放的是红桃![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃![]() 或黑桃
或黑桃![]() B. 红桃
B. 红桃![]() 或梅花
或梅花![]()
C. 黑桃![]() 或方片
或方片![]() D. 黑桃
D. 黑桃![]() 或梅花
或梅花![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
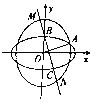
【题目】如图,椭圆![]() :
: ![]()
![]() 的焦距与椭圆
的焦距与椭圆![]() :
: ![]() 的短轴长相等,且
的短轴长相等,且![]() 与
与![]() 的长轴长相等,这两个椭圆在第一象限的交点为
的长轴长相等,这两个椭圆在第一象限的交点为![]() ,直线
,直线![]() 经过
经过![]() 在
在![]() 轴正半轴上的顶点
轴正半轴上的顶点![]() 且与直线
且与直线![]() (
(![]() 为坐标原点)垂直,
为坐标原点)垂直, ![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
, ![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求![]() 的标准方程;
的标准方程;
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com