
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
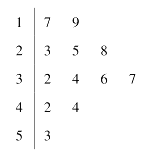
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;当月低于40万件没有奖励,用该样本估计总体,从电商平台一个年度内高于该年月销售平均数的月份中任取两个月,求这两个月企业发给电商平台的奖金为20万元的概率.
【答案】(1)中位数为33(万件),平均数为32.5;(2)![]()
【解析】
(1)由茎叶图可知,12个数据中间两个数据为32,34,所以中位数为33,由平均数公式可计算出电商平台的月销售数量的平均数;
(2)一年内月销售量高于平均数的月份有6个,其中这6个月能获奖励的月份有3个月,记为![]() ,不能获奖励的份为
,不能获奖励的份为![]() ,列举出从这6个月抽出的两个月的所有可能情况,再找出抽到的两个月都获奖励的可能情况,根据古典概型的概率公式即可求出.
,列举出从这6个月抽出的两个月的所有可能情况,再找出抽到的两个月都获奖励的可能情况,根据古典概型的概率公式即可求出.
(1)由茎叶图知,电商平台的月销售数量的中位数为33(万件),
电商平台的月销售数量的平均数为:
![]() (万件).
(万件).
(2)由题知,一年内月销售量高于平均数的月份有6个,其中这6个月能获奖励的月份有3个月,记为![]() ,不能获奖励的份为
,不能获奖励的份为![]() .
.
记从一个年度内高于该年月销售平均数的月份中抽到的两个月都获奖励的事件为![]() .
.
则从一个年度内高于该年月销售平均数的月份中抽出的两个月的所有可能为:
![]()
![]()
![]()
![]()
![]() .
.
共有15种可能.抽到的两个月都获奖励的可能为:![]() ,共有3种,所以
,共有3种,所以![]() .
.
所以,这两个月企业发给电商平台的奖金为20万元的概率为![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】试比较下面概率的大小:
(1)如果以连续掷两次骰子依次得到的点数m,n作为点P的横、纵坐标,点P在直线![]() 的下面
的下面![]() 包括直线
包括直线![]() 的概率
的概率![]() ;
;
(2)在正方形![]() ,
,![]() ,x,
,x,![]() ,随机地投掷点P,求点P落在正方形T内直线
,随机地投掷点P,求点P落在正方形T内直线![]() 的下面
的下面![]() 包括直线
包括直线![]() 的概率
的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长与焦距分别为方程
的长轴长与焦距分别为方程![]() 的两个实数根.
的两个实数根.
(1)求椭圆的标准方程;
(2)若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() ,
,![]() 两点,
两点,![]() 是椭圆的左焦点,当
是椭圆的左焦点,当![]() 面积最大时,求直线
面积最大时,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某公司举行大型抽奖活动,活动中准备了一枚质地均匀的正十二面体的骰子,在其十二个面上分别标有数字1,2,3,…,12,每位员工均有一次参与机会,并规定:若第一次抛得向上面的点数为完全平方数(即能写成整数的平方形式,如![]() ),则立即视为获得大奖;若第一次抛得向上面的点数不是完全平方数,则需进行第二次抛掷,两次抛得的点数和为完全平方数(如
),则立即视为获得大奖;若第一次抛得向上面的点数不是完全平方数,则需进行第二次抛掷,两次抛得的点数和为完全平方数(如![]() ),也可视为获得大奖.否则,只能获得安慰奖.
),也可视为获得大奖.否则,只能获得安慰奖.
(1)试列举须抛掷两次才能获得大奖的所有可能情况(用![]() 表示前后两次抛得的点数),并说明所有可能情况的总数;
表示前后两次抛得的点数),并说明所有可能情况的总数;
(2)若获得大奖的奖金(单位:元)为抛得的点数或点数和(完全平方数)的360倍,而安慰奖的奖金为48元,该公司某位员工获得的奖金为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,AC=![]() BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
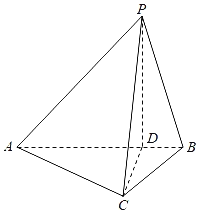
(1)求证:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有下列四个结论,其中所有正确结论的编号是___________.
①若![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差数列
是等差数列![]() 的前
的前![]() 项,则
项,则![]() ;
;
③“![]() ”的一个必要不充分条件是“
”的一个必要不充分条件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com