
| A. | $\frac{3\sqrt{6}}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 充分利用平面几何图形的性质解题.因从同一点出发的切线长相等,记△PF1F2的边PF1、PF2、F1F2上的切点分别为K、N、D,得PK|=|PN|,|F1K|=|F1D|,|F2N|=|F2D|,再结合双曲线的定义得|F1D|-|F2D|=2a,从而即可求得△PF1F2的内心的横坐标,即有M的坐标,运用点到直线的距离公式,可得a,b的关系,再由离心率公式计算即可得到所求值.
解答 解:记△PF1F2的边PF1、PF2、F1F2上的切点分别为K、N、D,
易见M、D横坐标相等,
|PK|=|PN|,|F1K|=|F1D|,|F2N|=|F2D|,由|PF1|-|PF2|=2a,
即:|PK|+|KF1|-(|PN|+|NF2|)=2a,得|KF1|-|NF2|=2a即|F1D|-|F2D|=2a,
记M的横坐标为x0,则D(x0,0),
于是:x0+c-(c-x0)=2a,得x0=a,
可得M(a,b+$\frac{b}{a}$),
由点M到直线y=$\frac{b}{a}$x的距离为$\frac{1}{2}$,
即为$\frac{|ab-ab-b|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{1}{2}$,
化为a=$\sqrt{3}$b,
即有c2=a2+b2=a2+$\frac{1}{3}$a2=$\frac{4}{3}$a2,
可得e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故选:D.
点评 本题考查双曲线的定义、方程和性质,主要是离心率的求法,注意运用切线的性质判断圆心的横坐标是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
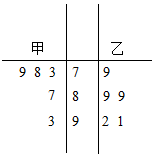 甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )
甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )| A. | $\overline{x_1}$>$\overline{x_2}$,乙比甲成绩稳定 | B. | $\overline{x_1}$>$\overline{x_2}$,甲比乙成绩稳定 | ||
| C. | $\overline{x_1}$<$\overline{x_2}$,乙比甲成绩稳定 | D. | $\overline{x_1}$<$\overline{x_2}$,甲比乙成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
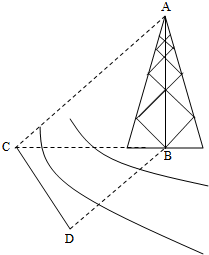 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 30$\sqrt{2}$米 | B. | 30$\sqrt{6}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 10$\sqrt{6}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z | B. | x=kπ+$\frac{π}{8}$,k∈Z | C. | x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z | D. | x=kπ+$\frac{3π}{8}$,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\sqrt{6}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com