
【题目】试比较3-![]() 与
与![]() (n为正整数)的大小,并予以证明.
(n为正整数)的大小,并予以证明.
【答案】见解析
【解析】
利用作差法可得3-![]() -
-![]() =
=![]() ,确定3-
,确定3-![]() 与
与![]() 的大小关系等价于比较
的大小关系等价于比较![]() 与2n+1的大小,利用数学归纳法证明即可.
与2n+1的大小,利用数学归纳法证明即可.
证明:3-![]() -
-![]() =
=![]() ,
,
于是确定3-![]() 与
与![]() 的大小关系等价于比较
的大小关系等价于比较![]() 与2n+1的大小.
与2n+1的大小.
由2<2×1+1,![]() <2×2+1,
<2×2+1,![]() >2×3+1,
>2×3+1,![]() >2×4+1,
>2×4+1,![]() >2×5+1,
>2×5+1,
可猜想当n≥3时,![]() >2n+1,
>2n+1,
证明如下:
ⅰ当n=3时,由上可知显然成立.
ⅱ假设当n=k时,![]() >2k+1成立.
>2k+1成立.
那么,当n=k+1时,
![]() =2×
=2×![]() >2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1,
>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1,
所以当n=k+1时猜想也成立,
综合ⅰ和ⅱ,对一切n≥3的正整数,都有![]() >2n+1.
>2n+1.
所以当n=1,2时,3-![]() <
<![]() ;
;
当n≥3时,3-![]() >
>![]() (n为正整数).
(n为正整数).


科目:高中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
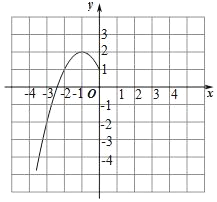
(3)观察函数图象,写出两条函数的性质./p>
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一平面内有两个边长都是2的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为______.
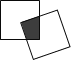
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织数学学科考试,随机抽取50名学生(满分150分,且抽取的学生成绩都在![]() 内)的成绩并制成频率分布直方图如图所示.
内)的成绩并制成频率分布直方图如图所示.
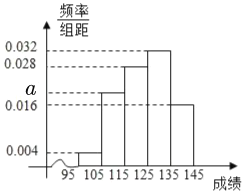
(1)根据频率分布直方图,估计这50名同学的数学平均成绩;(同一组中的数据以该组区间的中点值作代表)
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学的数学成绩在同一组中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com