
【题目】随着生活水平的逐步提高,人们对文娱活动的需求与日俱增,其中观看电视就是一种老少皆宜的娱乐活动.但是我们在观看电视娱乐身心的同时,也要注意把握好观看时间,近期研究显示,一项久坐的生活指标——看电视时间,是导致视力下降的重要因素,即看电视时间越长,视力下降的风险越大.研究者在某小区统计了每天看电视时间![]() (单位:小时)与视力下降人数
(单位:小时)与视力下降人数![]() 的相关数据如下:
的相关数据如下:
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
(1)请根据上面的数据求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(2)我们用(1)问求出的线性回归方程![]() 的
的![]() 估计回归方程
估计回归方程![]() ,由于随机误差
,由于随机误差![]() ,所以
,所以![]() 是
是![]() 的估计值,
的估计值,![]() 成为点(
成为点(![]() ,
,![]() )的残差.
)的残差.
①填写下面的残差表,并绘制残差图;
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
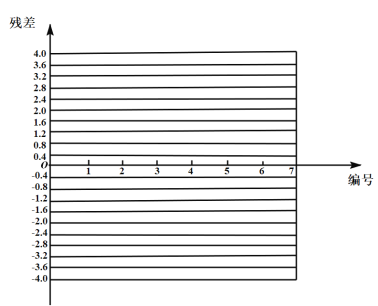
②若残差图所在带状区域宽度不超过4,我们则认为该模型拟合精度比较高,回归方程的预报精度较高,试根据①绘制的残差图分折该模型拟合精度是否比较高?
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为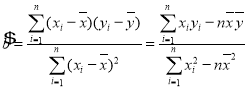 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某地位于甲、乙两条河流的交汇处,根据统计资料预测,今年汛期甲河流发生洪水的概率为0.25,乙河流发生洪水的概率为0.18(假设两河流发生洪水与否互不影响).现有一台大型设备正在该地工作,为了保护设备,施工部门提出以下三种方案:
方案1:运走设备,此时需花费4000元;
方案2:建一保护围墙,需花费1000元,但围墙只能抵御一个河流发生的洪水,当两河流同时发生洪水时,设备仍将受损,损失约56000元;
方案3:不采取措施,此时,当两河流都发生洪水时损失达60000元,只有一条河流发生洪水时,损失为10000元.
(1)试求方案3中损失费X(随机变量)的分布列;
(2)试比较哪一种方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李先生家住![]() 小区,他工作在
小区,他工作在![]() 科技园区,从家开车到公司上班路上有
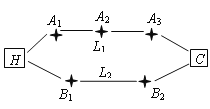
科技园区,从家开车到公司上班路上有![]() 两条路线(如图),
两条路线(如图),![]() 路线上有
路线上有![]() 三个路口,各路口遇到红灯的概率均为
三个路口,各路口遇到红灯的概率均为![]() ;
;![]() 路线上有
路线上有![]() 两个路口,各路口遇到红灯的概率依次为
两个路口,各路口遇到红灯的概率依次为![]() .
.
(Ⅰ)若走![]() 路线,求最多遇到1次红灯的概率;
路线,求最多遇到1次红灯的概率;
(Ⅱ)若走![]() 路线,求遇到红灯次数
路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
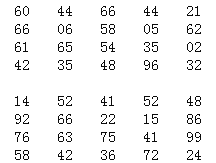
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]()
(1)求抛物线![]() 的方程,并求其焦点坐标与准线方程;
的方程,并求其焦点坐标与准线方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() 过点
过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() 为坐标原点.若
为坐标原点.若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为
(a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F1的直线l交椭圆于A,B两点,当△ABF2面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直四棱柱![]() 中,底面
中,底面![]() 是边长为6的正方形,点
是边长为6的正方形,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,过点
,过点![]() 作直四棱柱
作直四棱柱![]() 外接球的截面,所得的截面面积的最大值与最小值之差为
外接球的截面,所得的截面面积的最大值与最小值之差为![]() ,则直四棱柱
,则直四棱柱![]() 外接球的半径为( )
外接球的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com