
| A. | $\frac{4π}{3}$ | B. | 4π | C. | 8π | D. | 20π |
分析 由已知结合三棱锥和正三棱柱的几何特征,可得此三棱锥外接球,即为以△ABC为底面以PA为高的正三棱柱的外接球,分别求出棱锥底面半径r,和球心距d,代入R=$\sqrt{{r}^{2}+{d}^{2}}$,可得球的半径R,由此能求出该三棱锥外接球的表面积.
解答 解:根据已知中底面△ABC是边长为$\sqrt{3}$的正三角形,PA⊥底面ABC,
可得此三棱锥外接球,即为以△ABC为底面以PA为高的正三棱柱的外接球
∵△ABC是边长为$\sqrt{3}$的正三角形,
∴△ABC的外接圆半径r=$\frac{2}{3}\sqrt{3-\frac{3}{4}}$=1,
球心到△ABC的外接圆圆心的距离d=1,
故球的半径R=$\sqrt{{r}^{2}+{d}^{2}}$=$\sqrt{2}$,
故三棱锥P-ABC外接球的表面积S=4πR2=8π,
故选:C.
点评 本题考查的知识点是球内接多面体,熟练掌握球的半径R公式R=$\sqrt{{r}^{2}+{d}^{2}}$,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
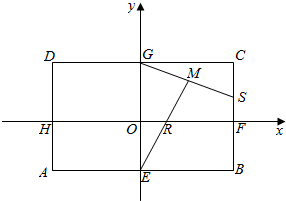 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 所有的质数都是奇数 | B. | ?x∈R,2x2+2≥2 | ||
| C. | 对每一个无理数x,x2也是无理数 | D. | 所有长度相等的向量均相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-e,-1) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7h2-h | B. | 14xh-6x+2 | C. | xh+h2+h | D. | h(14x+7h-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com