
����Ŀ�����������ֻ����ռ���ʹ���ֻ�������Ϊ�������ճ������һ���֣��ܶ������߶��ֻ�����������Խ��Խ��.��ɳijͨ�Ź�˾Ϊ�˸��õ����������߶��������������Ƴ�һ��������.��ͨ�Ź�˾ѡ��5�����У������������÷�չ��������������ȷ���ȽϽӽ������ò�ͬ�Ķ��۷�����Ϊ�Ե㣬����һ���µ�ͳ�ƣ����ָ��������Ķ���![]() :(��λ��Ԫ/�£���������
:(��λ��Ԫ/�£���������![]() (��λ�����ˣ��Ĺ�ϵ���:
(��λ�����ˣ��Ĺ�ϵ���:
![]()
��1�����ݱ��е����ݣ��������ϵ�����з���˵�����Ƿ���������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ����ָ��������ػ��Ǹ���أ�
�Ĺ�ϵ����ָ��������ػ��Ǹ���أ�
��2�������![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
������ͨ�Ź�˾��һ���������Ե�ij����н�����������ļ۸�λ25Ԫ/ �£���������ع鷽��Ԥ�ⳤɳ��һ�����ڹ�����������������ܷ�20 ����.
�ο����ݣ�![]() ��
��![]() ��
��![]() .
.
�ο���ʽ�����ϵ��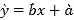 ���ع�ֱ�߷���
���ع�ֱ�߷���![]() ��
��
����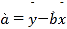 ��
��![]() .
.
���𰸡�(1)������;(2)��![]() ;��һ�����ڹ�����������������ᳬ��20����.
;��һ�����ڹ�����������������ᳬ��20����.
��������
(1) �������⣬��![]() ,
,![]() ��������ϵ��
��������ϵ��![]() ���Ӷ����������ж�;
���Ӷ����������ж�;
(2) ������ع�ֱ�߷��̣����ɢ�֪����![]() ����
����![]() ���Ӷ�Ԥ�ⳤɳ��һ�����ڹ�����������������ᳬ��20����
���Ӷ�Ԥ�ⳤɳ��һ�����ڹ�����������������ᳬ��20����
��1���������⣬��![]() ��
��
![]() .
.
�������
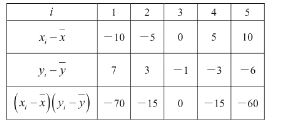
���ݱ���Ͳο����ݣ���![]() ��
��
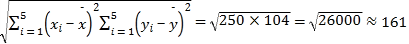 .
.
������ϵ��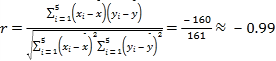 .
.
����![]() �ܽӽ�1��������������Իع鷽��ģ�����
�ܽӽ�1��������������Իع鷽��ģ�����![]() ��
��![]() �Ĺ�ϵ.
�Ĺ�ϵ.
����![]() �������ϵΪ�����.
�������ϵΪ�����.
��2����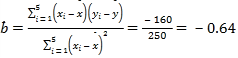 ��
��![]() ��
��
���![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() .
.
���ɢ�֪����![]() ����
����![]() ���������������ļ۸�Ϊ25Ԫ/�£���Ԥ�ⳤɳ��һ�����ڹ�����������������ᳬ��20����.
���������������ļ۸�Ϊ25Ԫ/�£���Ԥ�ⳤɳ��һ�����ڹ�����������������ᳬ��20����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ����
����![]() .
.
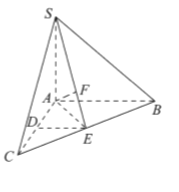
��I����֤��![]() ��
��
��II����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��III�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ�����
��ʹ�����![]() �Ĵ�СΪ
�Ĵ�СΪ![]() �������ڣ����
�������ڣ����![]() �ij����������ڣ���˵������.
�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰn���
��ǰn���![]() ��
�� ![]() �ǵȲ����У���
�ǵȲ����У���![]() .
.
������������![]() ��ͨ�ʽ��
��ͨ�ʽ��
�������� .������
.������![]() ��ǰn���
��ǰn���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ʋ����ˣ�δ��7��һ��оƬ����������ȴ�������й���о�����о��ȳ�.ij��˾�ף��ң��������з�С��ֱ��з�![]() ��
��![]() ��
��![]() ���ֲ�ͬ��оƬ�������÷ֲ�����ķ�������ЩоƬ�г�ȡ���ɼ����������������й����ݼ��±�����λ������.
���ֲ�ͬ��оƬ�������÷ֲ�����ķ�������ЩоƬ�г�ȡ���ɼ����������������й����ݼ��±�����λ������.
оƬ | ���� | ��ȡ���� |
| 200 |
|
| 600 |
|
| 400 | 2 |
������![]() ��ֵ��
��ֵ��
����������������Ʒ�������ȡ2������ij�������н�һ����⣬����2��оƬ���Բ�ͬ����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD�������Σ�E��F�ֱ�ΪPC��BD���е㣬����PAD�͵���ABCD��
��1����֤��EF��ƽ��PAD��
��2����EF��PC����֤��ƽ��PAB��ƽ��PCD��
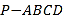
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ���ص��ҳ�Ϊ
���ص��ҳ�Ϊ![]() .
.
��1����Բ�ĵ�ֱ��![]() �ľ��룻
�ľ��룻
��2����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ı߳�Ϊ4��
�ı߳�Ϊ4��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬��
���е㣬��![]() Ϊ�⽫������
Ϊ�⽫������![]() �۳���ͼ��ʾ��
�۳���ͼ��ʾ��![]() �Ķ���ǣ���
�Ķ���ǣ���![]() ���߶�
���߶�![]() ���Ҳ����
���Ҳ����![]() ��
��![]() �غϣ�ֱ��
�غϣ�ֱ��![]() ����
����![]() ��
��![]() ��
��![]() ������ȷ����ƽ���ཻ������Ϊ
������ȷ����ƽ���ཻ������Ϊ![]() ��
��
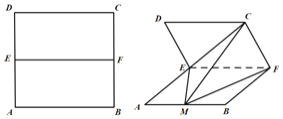
��1����![]() Ϊ
Ϊ![]() ���е㣬��ȷ����
���е㣬��ȷ����![]() ��λ�ã���֤��ֱ��
��λ�ã���֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ����
����![]() �ij��ȣ������ʱ��
�ij��ȣ������ʱ��![]() ��ƽ��
��ƽ��![]() �ľ��룮
�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����Ϊ����ԭ��O,�Գ���Ϊ������,�ҹ�M��2�� ![]() �� ��N(
�� ��N(![]() ,1)���㣬
,1)���㣬
��I������Բ�ķ��̣�
��II���Ƿ����Բ����ԭ���Բ��ʹ�ø�Բ������һ����������ԲC������������A,B,��![]() �������ڣ�д����Բ�ķ��̣�����|AB |��ȡֵ��Χ����������˵�����ɡ�
�������ڣ�д����Բ�ķ��̣�����|AB |��ȡֵ��Χ����������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ABCD�Ķ��㶼����O�������ϣ�����ABCD�DZ߳�Ϊ2�������Σ���PA����ABCD�������������Ϊ![]() �����������Ϊ_____��
�����������Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com