
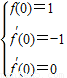 £¬µĂ
£¬µĂ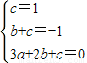 £¬ÓÉ´ËÄÜÇó³öf£¨x£©µÄ½âÎöʽ£®
£¬ÓÉ´ËÄÜÇó³öf£¨x£©µÄ½âÎöʽ£®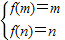 £¬°ÑÎỀâת»¯Îª£¨x-1£©2ex-x=0ÓĐÁ½¸ö´óÓÚ1µÄ²»µÈʵ¸ù£¬ÓÉ´ËÄÜÍƵ¼³öµ±x£¾1ʱ£¬f£¨x£©²»´æÔÚ¡°±£ÖµÇø¼ä¡±£®
£¬°ÑÎỀâת»¯Îª£¨x-1£©2ex-x=0ÓĐÁ½¸ö´óÓÚ1µÄ²»µÈʵ¸ù£¬ÓÉ´ËÄÜÍƵ¼³öµ±x£¾1ʱ£¬f£¨x£©²»´æÔÚ¡°±£ÖµÇø¼ä¡±£®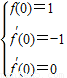 £¬
£¬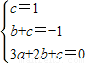 £¬
£¬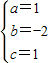 £®
£® £¬
£¬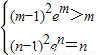 £¬
£¬| x | £¨1£¬x£© | x | £¨x£¬+¡̃£© |
| h¡ä£¨x£© | - | 0 | + |
| h£¨x£© | ¡ư | ¼«Đ¡Öµ | ¡ü |


 Đ¿αê½×̀ƯÔĶÁѵÁ·ÏµÁĐ´đ°¸
Đ¿αê½×̀ƯÔĶÁѵÁ·ÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
| ¦Đ |
| 4 |
| ¦Đ |
| 6 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
| 1 |
| x |
| m |
| 2 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
| 1 |
| f(n) |
A¡¢
| ||
B¡¢
| ||
C¡¢
| ||
D¡¢
|
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
²é¿´´đ°¸ºÍ½âÎö>>
°Ù¶ÈÖÂĐÅ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com