
���� ��1������$a_n^2-{a_n}{a_{n-1}}-2n{a_{n-1}}-4{n^2}=0$����n��2��n��N��д���𰸼��ɣ�
��2������֪�����õ���an+2n����an-an-1-2n��=0���ɴ����${a_n}-{a_{n-1}}-2n=0\begin{array}{l}{\;}{��n��2��}\end{array}$������an=��an-an-1��+��an-1-an-2��+��+��a2-a1��+a1��
��3������������bn=$\frac{1}{��2n+\frac{1}{n}��}+3$��Ȼ�����û�Ԫ���õ���$f��x��=2x+\frac{1}{x}$��x��1�������䵼����Ϊ$f'��x��=2-\frac{1}{x^2}��2-1��0$����Ϻ����ĵ����Խ��н��
��� �⣺��1��a2=6��a3=12��
��2������֪�ɵã���an-2n����an+2n��-an-1��an+2n��=0��
�ࣨan+2n����an-an-1-2n��=0��
��an��0��
��${a_n}-{a_{n-1}}-2n=0\begin{array}{l}{\;}{��n��2��}\end{array}$��
��an=��an-an-1��+��an-1-an-2��+��+��a2-a1��+a1=2+4+6+��+2n=n��n+1����
��3��${b_n}=\frac{1}{{{a_{n+1}}}}+\frac{1}{{{a_{n+2}}}}+\frac{1}{{{a_{n+3}}}}+��+\frac{1}{{{a_{2n}}}}$
=$\frac{1}{��n+1����n+2��}+\frac{1}{��n+2����n+3��}+��+\frac{1}{2n��2n+1��}$
=$\frac{1}{n+1}-\frac{1}{2n+1}=\frac{n}{{2{n^2}+3n+1}}=\frac{1}{{��2n+\frac{1}{n}��+3}}$��
��$f��x��=2x+\frac{1}{x}$��x��1������$f'��x��=2-\frac{1}{x^2}��2-1��0$��
����f��x����[1��+�ޣ�������������
�ʵ�x=1ʱ��f��x��ȡ����Сֵ3������n=1ʱ��${��{b_n}��_{max}}=\frac{1}{6}$��
${t^2}-2mt+\frac{1}{6}��{b_n}$��?n��N*��?m��[-1��1]��$?{t^2}-2mt+\frac{1}{6}��{��{b_n}��_{max}}=\frac{1}{6}$��
��t2-2mt��0��?m��[-1��1]��$?\left\{\begin{array}{l}{t^2}-2t��0\\{t^2}+2t��0\end{array}\right.$��
��֮�ã�ʵ��t��ȡֵ��ΧΪ��-�ޣ�-2���ȣ�2��+�ޣ���
���� �������е�ͨ�ʽ��������ʵ����ȡֵ��Χ�������е��⣬����ʱҪ�������⣬ע�⺯�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{3}$ | B�� | $\sqrt{7}$ | C�� | $\sqrt{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
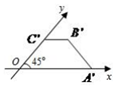 һֱ�����ε�ֱ��ͼ��һ����ͼ��ʾ�����Σ���OA��=2��B��C��=OC��=1�����ֱ�����ε����Ϊ��������
һֱ�����ε�ֱ��ͼ��һ����ͼ��ʾ�����Σ���OA��=2��B��C��=OC��=1�����ֱ�����ε����Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ͦ£���m��n | B�� | �����Φ£���m��n | C�� | ��m��n������ͦ� | D�� | ��n�ͦ�������ͦ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com