
【题目】若数列![]() 满足:对于任意
满足:对于任意![]() ,
,![]() 均为数列
均为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() ,试判断数列
,试判断数列![]() 是否为“
是否为“![]() 数列”?说明理由;
数列”?说明理由;
(2)若公差为![]() 的等差数列
的等差数列![]() 为“
为“![]() 数列”,求
数列”,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 为“
为“![]() 数列”,
数列”,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)不是,见解析(2)![]() (3)
(3)![]()
【解析】
(1)利用递推关系求出数列的通项公式,进一步验证![]() 时,
时,![]() 是否为数列
是否为数列![]() 中的项,即可得答案;
中的项,即可得答案;
(2)由题意得![]() ,再对公差进行分类讨论,即可得答案;
,再对公差进行分类讨论,即可得答案;
(3)由题意得数列![]() 为等差数列,设数列
为等差数列,设数列![]() 的公差为
的公差为![]() ,再根据不等式
,再根据不等式![]() 得到公差的值,即可得答案;
得到公差的值,即可得答案;
(1)当![]() 时,
时,![]()
又![]() ,所以
,所以![]() .
.
所以![]()
当![]() 时,
时,![]() ,而
,而![]() ,
,
所以![]() 时,
时,![]() 不是数列
不是数列![]() 中的项,故数列
中的项,故数列![]() 不是为“
不是为“![]() 数列”
数列”
(2)因为数列![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,
所以![]() .
.
因为数列![]() 为“
为“![]() 数列”
数列”
所以任意![]() ,存在
,存在![]() ,使得
,使得![]() ,即有
,即有![]() .
.
①若![]() ,则只需
,则只需![]() ,使得
,使得![]() ,从而得
,从而得![]() 是数列
是数列![]() 中的项.
中的项.
②若![]() ,则
,则![]() .此时,当
.此时,当![]() 时,
时,![]() 不为正整数,所以
不为正整数,所以![]() 不符合题意.综上,
不符合题意.综上,![]() .
.
(3)由题意![]() ,所以
,所以![]() ,
,
又因为![]() ,且数列
,且数列![]() 为“
为“![]() 数列”,
数列”,
所以![]() ,即
,即![]() ,所以数列
,所以数列![]() 为等差数列.
为等差数列.
设数列![]() 的公差为
的公差为![]() ,则有
,则有![]() ,
,
由![]() ,得
,得![]() ,
,
整理得![]() ,①
,①
![]() .②
.②
若![]() ,取正整数
,取正整数![]() ,
,
则当![]() 时,
时,![]() ,
,
与①式对应任意![]() 恒成立相矛盾,因此
恒成立相矛盾,因此![]() .
.
同样根据②式可得![]() ,
,
所以![]() .又
.又![]() ,所以
,所以![]() .
.
经检验当![]() 时,①②两式对应任意
时,①②两式对应任意![]() 恒成立,
恒成立,
所以数列![]() 的通项公式为
的通项公式为![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的一个焦点为
)的一个焦点为![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)过点![]() 且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为
且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为![]() ,
,![]() ,
,![]() 与
与![]() 相交于点Q,求证:点Q在某条定直线上.
相交于点Q,求证:点Q在某条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线![]() 至少经过其样本数据
至少经过其样本数据![]() 中的一个点
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
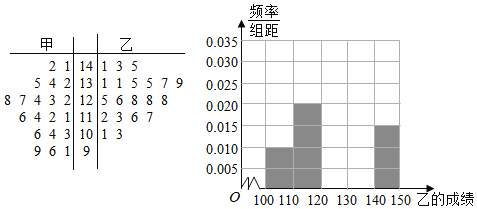
(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com